|
Oberon #05
06 ноября 1998 |
|
(C) ALK/Stars of Keladan H.G. MMA> Слышь, Шурик, сделай статью про фракталы. ALK> Да зачем, всё равно никто не заинте- ресуется ими... MMA> Ну тогда общественность,увидев очере- дной фрактал в деме, будет говорить: А, это опять с Амиги таблички стянули и строят по ним Папоротники и эти... Мандельброты... ...Вот тут-то меня и задело, можно сказать, за живое. Что делать, положение обязывает раскрыть наконец-то всю правду о фракталах.Начнём, как всегда, с определений. Fractus (лат.) - ломаный, дробный. Фрактал, в приложении к математике, есть некий объект, описываемый простыми цикли- ческими (или рекурсивными) формулами,и ко- торый, самое главное, копирует самого себя при изменении масштаба вычислений. Но это определение. а как на практике ? Дело в том, что фракталы существуют не только "на бумаге", они есть везде. Напри- мер, кровеносная система - артерия на про- тяжении всей длины ветвится и уменьшается в диаметре, каждая новая ветвь похожа на предыдущую, также ветвится и уменьшается. Если бы не предел размера клеток, это ветвление продолжалось бы до бесконечнос- ти. Но это "простой" фрактал. Есть послож- нее, например, лист дерева. Если внима- тельно присмотреться к прожилкам на листе, то можно заметить, что каждая из них пов- торяет главное "соцветие" из самых боль- ших. И точно также можно сказать, приняв "вторичные соцветия" за главные. Можно самому придумать искусственный фрак- тал - например нарисуйте квадрат, вокруг его вершин нарисуйте ещё четыре квадрата со стороной в 2-3 раза меньшей, чем у ква- драта-родителя. Повторите эту операцию раз 50 для каждого из поколений квадратов.:[ ] Не устали? ;) А теперь посмотрите на это творение - красиво, не правда-ли ? Красота - вот в чём сила фракталов, она завораживает своей простотой и бЕСКОНЕЧНОСТьЮ! А тем более, вооружившись компьютером вместо бумаги, можно творить такие пейзажи!
Фрактал Мандельброта. Вот его формула: Z(i+1)=Z(i)*Z(i)+C, где: Z - комплексная переменная: C - комплексная константа: (i),(i+1) - шаги вычислений, итераций.
Те, кому не довелось изучать страшный предмет "Высшая Математика", наверняка уже "загрузились" и считают, что это настолько сложно для их понимания, что не стоит и читать весь этот дальнейший бред. Не спешите ! Я постараюсь объяснить... ...не берусь быть абсолютно точным, буду предельно краток. Комплексное число Z можно представить как: Z=а+j*b, где а,b - простые обычные числа, j - мнимая единица, не стану забивать вам голову этим отстоем,но как ни удивительно, j. умноженная на такую же j. равна МИНУС ОДНОМУ. Аналогично. корень из -l (маразм. да?) будет равен j. Если обычные числа принято графически ото- бражать на числовой ПРЯМОЙ, то вот такие извратные - на числовой ПЛОСКОСТИ. Эти числа имеют две координаты, реальную (а), и мнимую (b), которые и откладываются соответственно по X и Y - осям на плоскос- ти. Точка пересечения этих отсчётов и есть это КОМПЛЕКСНОЕ ЧИСЛО.
Чувствуете, куда я клоню ? Всё это дело можно (и нужно!) отображать на плоскости, а именно на плоскости экрана. Вопрос, как! Для построения фрактала Мандельброта необ- ходимо перебрать все точки на нашей плос- кости на предмет соответствия следующему условию. В цикле от l до l0000 (не меньше!) необхо- димо рассчитывать последовательность: A:=а*а-b*b+х В:=2*а*b+y а:=A b:=В R:=SQR(а*а+b*b) i:=i+1 Первые две строки - не что иное, как ви- денная вами ранее формула Z:=z*z+c, но за- писанная "нормальным" языком. Пояснение: а и b - реальная и мнимая части числа Z, х и y - это соответственно реальная и мнимая составляющие комплексного числа C. В нашем случае - это координаты той точки, которую необходимо рассчитать. По ходу вычислений для одной точки х и y не изменяются. Следующие две строки скорее нужны только для ясности - после вычисления A и В производится присвоение новых результатов в исходные для следующего цикла. Предпоследняя строка - самое важное.Это не что иное, как УСЛОВИЕ, при котором нужно остановить цикл. Логично предположить, что здесь подсчитывается общий "размер" числа Z, его величина. Вот тут начинается самое интересное. Оказывается, для разных исход- ных точек на плоскости размер R в цикле расчёта будет "вести" себя по-разному. Для некоторых точек здесь будет какая-то пос- тоянная величина, для других значение R будет стремительно "улетать" в +/- беско- нечность. Оценивая, с какой скоростью "улетает" точка в бесконечность,можно гра- фически отобразить её соответствующим цве- том на плоскости. Для компьютерного расчё- та здесь введена последняя строка того цикла i:=i+1. По количеству шагов, сделан- ной программой, можно судить о скорости "улетания" точки - чем меньше циклов, тем быстрее (ярче, но не факт) точка на плос- кости улетает в бесконечность. Перед пер- вым циклом, разумеется, значения а,b,i об- нуляются. Но тут возникает проблема - компьютер "не знает", что такое бесконеч- ность, вернее знает, но тогда уже поздно - сообщение типа Number too big не замедлит появиться. Здесь необходимо принять сле- дующее допущение: за "бесконечность" при- нимается ну очень большое число. Да, ещё о пределах. Для расчёта всех точек на плос- кости нужно всё-таки выбрать, ПДЕ рассчи- тывать. А рассчитывать нужно в пределах: от -2.S и до +l.S для х-, от -2 и до +2 для y-составляющей числа C, т.е. вблизи начала координат - именно там происходят "фрактальные коллизии", в ос- тальной области плоскости не происходит ничего интересного. ГДЕ вы будете рассчи- тывать и с каким ШАГОМ перебирать точки на плоскости (т.е. с каким увеличением) - это вопрос чисто творческий. "Всё это прекрасно", - скажете вы, "но при чём тут СПЕКТРУМ, только идиот будет рассчитывать 10000 циклов для каждой точки плоскости размером 256*192. Мало того, что эта хреновина будет считать два дня на BASIC'е, так ещё и неизвестно, как отобра- жать точки цветом!" Не отчаивайтесь, я с полной ответствен- ностью заявляю: Мандельброт на СПЕКТРУМе - реальность. Не нужно ждать два дня - мину- та от силы! А цвет - у нас же есть АТРИБУ- ТЫ цвета! Естественно, никакого BASIC'а. Код, и только код. На диске вы найдёте исходный текст "mandelbr.C" с коммента- риями в ASCII-кодировке и аналогичный "mandelbr.XAS" (без комментариев) для XAS- ассемблера. Я не претендую на то, что мат. процедуры там "самые крутые", но зато они МОИ !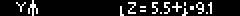
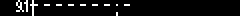
Вы думаете это всё, на что я был способен? Если да, то жмите "EXIT". А нет - "кончай- те эти сопли. вас ждёт ВТОРАЯ серия!" © mr.SECOND Фрактал Жюлиа (Julia). Формула: Z(i+1)=Z(i)*Z(i)+C
Как вы, наверное, уже заметили, эта форму- ла точь-в-точь повторяет формулу фрактала Мандельброта. И это неудивительно - ведь Мандельброт и Жюлиа - близнецы-братья. мы говорим "Мандельброт". подразумеваем - party... ;) ...Был такой мужик, из фирмы IBM, он его придумал, и стал изучать с помощью компь- ютера (отгадаете с двух раз, какого?): Ну а насчёт Жюлиа мне ничего неизвестно, ве- роятно, это был друг Мандельброта :), и он впервые посмотрел на "детище" немного с другой точки зрения: Если за начальное условие итерации принять Z(0)=0, и изменять C-константу от точки к точке, то получается фрактал Мандельброта, о чём я безуспешно :) пытался рассказать выше:
Наоборот, если принять C заМножества Жюлиа больше подходят под определение фрактала - как бы мы не "уве- личивали" масштаб изображения, мы будем созерцать одну и ту же картину, разве что будет смещаться цветовая гамма, а этого не скажешь о Мандельброте - при увеличении картина и форма всё-же изменяются. Если посмотреть с практической точки зре- ния, то с помощью Жюлиа-Мандельброта можно проделывать следующее: Zooming - рассчитывать изображение "вглубь", изменяя на каждом шаг "перебора" точек. На Спектруме это дело лучше рассчи- тать заранее, а затем... показывать как анимацию, поверьте, это будет выглядеть круто, что вы и могли видеть в демах EYE ACHE II/CBS (там был Мандельброт) и INSANE /ЗSC HARDCORE (тот-же Мандельброт). Morphing - для фрактала Мандельброта на каждом кадре можно изменять критерий оцен- ки "бесконечности" и тогда при просмотре "фильма" можно видеть, как фрактал плавно превращается из правильного круга, искрив- ляясь в свой первозданный вид. ...для фрактала Жюлиа на каждом кадре мож- но плавно изменять параметр C, как одну, так и другую составлающие. Естественно, при небольшом изменении C форма фрактала изменится незначительно. Вот это, я вам скажу, не просто круто, а очень круто! При просмотре вы можете видеть, как буквально на пустом фоне "расцветает" фрактал, изви- ваясь и закручивась в немыслимые узоры. На Спектруме этого (пока :)) не сделано. Об- ладатели "голубого калькулятора" могли это видеть в РС-демах. Voxel Mapping - если абстрагироваться от цвета точек, составляющих фрактал, и при- нять "вес" точки не за цвет, а за высоту, то можно "показывать" фрактальные пейзажи не "сверху", а со стороны, двигаясь над рельефом фрактала, изредка поворачивая и меняя высоту "полёта". Ну что можно ска- зать? Это тоже неплохо, тем более, что на Спектруме Voxel Mapping'и были всякие - Multicolor (EYE ACHE II), Chunky (Refresh,Blame),Attribute (Insane). Но вот Fractal Voxel Mapping'а на Спектруме ещё не было, хотя удивительно, почему никто не догадался вместо рельефной карты подста- вить фрактальную? ...Ну а,так сказать, "для общего развития" можно представить фрактал Мандельброта- Жюлиа, как формулу: Z(i+1)=Z(i)^N+C, где ^N - это возведение в степень N, где N больше 2-х. Вобщем, математики тут будет ещё больше, вычисляться будет медленней, короче, на Спеке будет тормозить ужасно... ... но картинка будет выглядеть красиво!!! Фрактал "Папоротник" Аффинноe множество.константу, не изменяющуюся от
точки к точке, а изменять
Z(0), равное координате точ-
ки, то мы получим множество
Жюлиа...
Конечно, из-за того, что
констант C существует беско-
нечное количество, вид
фрактала Жюлиа _существенно_
зависит от константы C.
Львиная доля этих значений
"порождает" некрасивые фигуры
- что-то вроде пятен, слабо
различимых на основном фоне.
По своему собственному опыту
я могу сказать, что значения
C должны быть где-то в преде-
лах +/- 5, причём обе состав-
ляющие этого числа C (не за-
были?) в большинстве случаев
имеют противоположные знаки.
Кстати, те
процедуры, о
которых я
говорил вы-
ше, можно
переделать
для расчёта
Жюлиа. А
что касается
пределов на
комплексной
плоскости -
то они ос-
таются теми-
же,что и для
Мандельброта
Значение
константы
Julia:
C=0.36-j0.37
Данный фрактал рассчитывается по другому принципу, нежели семейство Мандельброта. Если для Мандельброта образ получается последовательно, точка за точкой, то для аффинных фракталов построение "последова- тельно-координатное". .................. ...... ' . Схема .... . . ' ' . папоротника .. ' . .. 0 ' .'. . .. . .' .' . '. ' . . . . ' ' . ' . 1 | 2 .' . .' ' ' ' . . '. .' . ' . ' 4-┐ '.......... . ' . . │ ...'''. '. 0 . . .┴'' '. 3 . .' . .' 0 '.........' ..' .' ....''' ''''''''.........'''''' Цифрой 0 обозначен большой лист - это на- ружные контуры папоротника: 1,2 и 3 - меньшие по размеру листья, кото- рые получаются из 0 поворотом, переносом и масштабированием: 4 - черешок, который на самом деле тоже подобен 0, но сильно сжат в поперечном на- правлении. Построение сводится к следющему: Имеется некое математическое преобразова- ние, о котором будет сказано ниже, с его помощью получаются координаты точки экра- на, в которую нужно поставить пиксель. Это преобразование зависит от координат преды- дущей точки и от так называемого вероят- ностного коэффициента. Если циклически вы- зывать это преобразование (порядка 1000- 4000 раз) и после каждого ставить на экран точку, то в конце концов получится карти- на, примерно напоминающая изображённую в начале раздела. Так как "фигур" четыре, то для построения необходимо использовать одну из четырёх формул: х(i+1) = а1*х(i) + b1*y(i) + e1 (1) y(i+1) = c1*х(i) + d1*y(i) + f1 х(i+1) = а2*х(i) + b2*y(i) + e2 (2) y(i+1) = c2*х(i) + d2*y(i) + f2 х(i+1) = а3*х(i) + b3*y(i) + e3 (3) y(i+1) = c3*х(i) + d3*y(i) + f3 х(i+1) = а4*х(i) + b4*y(i) + e4 (4) y(i+1) = c4*х(i) + d4*y(i) + f4 ху(i+1) и ху(i) - традиционно, следующее и предыдущие значения координаты: а,b,c,d,e,f - коэффициенты преобразования, четыре группы для каждого. Т.е. каждое преобразование задаётся 6-ю коэффициентами (а,b,c,d,e,f), а полная конфигурация будущего папоротника пол- ностью задаётся 24-мя параметрами. Теперь возникает вопрос, какое из четырёх преобразований использовать ? Использовать нужно все 4. На каждом шаге, естественно, используется только одно. Как выбирать - случайно, но не равномерно. Степень вероятности использования преобразования пропорциональна площади соответствующей фигуры. Сумма площадей условно равна 1 или 100%, соответственно сумма вероятностей должна быть тоже равна 1. Что же касается реализации этого на Спек- труме, то для папоротника имеем: ┌-┬-----┬-----┬-----┬-----┬-----┬-----┬--┐ │N│ а │ b │ c │ d │ e │ f │р │ ├-┼-----┼-----┼-----┼-----┼-----┼-----┼--┤ │1│ 0.00│ 0.00│ 0.00│ 0.16│ 0.00│ 0.00│ 1│ │2│ 0.85│ 0.04│-0.04│ 0.85│ 0.00│ 1.60│84│ │3│ 0.20│-0.26│ 0.23│ 0.22│ 0.00│ 1.60│07│ │4│-0.15│ 0.28│ 0.26│ 0.24│ 0.00│ 0.44│07│ └-┴-----┴-----┴-----┴-----┴-----┴-----┴--┘ Р - вероятность использования, в %% Реализовать вероятностное выполнение той или иной формулы просто: 1. Вычисляем случайное число в пределах 0- 255 (один байт, если реализуем на асме): 2. Если число меньше 3, то формула (1): 3. Если число меньше 21, то формула (3): 4. Если число меньше 39, то формула (4): 5. Иначе - осталась формула (2): 0 3 21 39 255 ├---┼--------┼--------┼-----------------┤ 3/256 18/256 18/256 (256-39)/256 1% 7% 7% 84% Откуда берутся коэффициенты? Для каждой фигуры 1-4 задаём по три координаты, это могут быть координаты начала и конца листа плюс ещё точка листа, наиболее удалённая от линии, соединяющей эти начало и конец. Таким образом, у нас имеется четыре систе- мы уравнений: ┌ х1 = х1*а1 + y1*b1 + e1 │ y1 = х1*c1 + y1*d1 + f1 │ х2 = х2*а1 + y2*b1 + e1 │ y2 = х2*c1 + y2*d1 + f1 │ х3 = х3*а1 + y3*b1 + e1 └ y3 = х3*c1 + y3*d1 + f1, где х123,y123 - заданные координаты(известны): а,b,c,d,e,f - неизвестные величины. Решив каждую систему из 6 уравнений с 6-ю неизвестными каждая, можно найти искомую группу параметров а,b,c,d,e,f для каждого листа. Как решать? Не знаю и не спрашивайте :) Ну... что знал - рассказал. Дерзайте, фракталы на Спектруме - вещь малоизучен- ная. ------══════════════════════════════------ * * * * * Р.S. Статья подготовлена по материалам: 1. Журнала "Техника-Молодёжи" N9,199X: 2. Собственных изысканий и наблюдений: 3. Программы Fractal eXtreme Explorer/РС: 4. Демок RiseDemo/GLOBAL Corp.,NOUMENON/я: 5. FAQ fido-конференции DEMO.DESIGN. Р.Р.S. Чуть не забыл, в шкатулке есть та- кая прога, FRACTALS называется. Буржуйская она, однако. Ну, вобщем, вы меня поняли...
Other articles:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Similar articles:
В этот день... 21 November