3.4.3. Представление плоской фигуры.
Будем считать такую фигуру n-угольником. Даже
если это и не так, например если мы имеем дело с окружностью, то ее
можно заменить п угольником с большим количеством вершин и малым
размером сторон.
прежде всего, нам конечно придется занести в
память координаты всех п вершин этой фигуры. Но этого еще, увы,
недостаточно. Дело в том, что мы еще ничего не знаем о сторонах. На
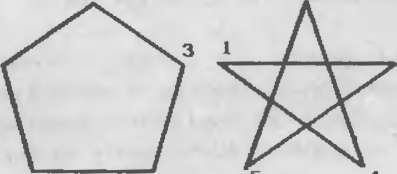
рис.38 показаны две совершенно непохожие друг на друга пятиугольные
фигуры, имеющие одинаковые координаты вершин.
2
2
5
4
5
4
Рис. 38 Две различные фигуры с одинаковыми координатами вершин
Таким образом, для задания плоской фигуры кроме массива
координат вершин необходимо организовать еще
массив, описывающий стороиы фигуры. Так, на рисунке 38 сторона 1-2 у
первой фигуры существует, а у второй - нет, зато там существует сторона
1-3, которой нет у первой фигуры.
Самый простой способ создать такой массив -
записать порядок обхода всех вершин многоугольника, начиная с любой.
При этом имеет смысл руководствоваться определенным порядком обхода,
например обходить вершины всегда только против часовой стрелки (где
такое правило может оказаться полезным, мы покажем далее) .
Тогда для первой фигуры (рис. 38) массив
описания сторон будет иметь вид: 1,2,2,3,3,4,4,5,5,1; а для второй
фигуры - соответственно : 1,3,3,5,5,2,2,4,4,1.
Написать программу (процедуру) для построения
фигуры, у которой заданы экранные координаты всех вершин и описаны
стороны, совсем несложно. Это можно сделать как на БЕИСИКе, так и в
кодах Способ реализации неважен. Важно то, как это организовано.
Для этой книги мы подготовили такую программу в
машинном коде, но при редактировании вынуждены были от нее отказаться,
т.к. эа большим размером самой программы теряется ее суть. Нам остается
только ограничиться демонстрационным примером на БЕЙ-сИКе, который
естественно работает далеко не плавно, но зато демонстрирует сам
принцип того, как задаются плоские фигуры
Демонстрационный пример.
Эта программа демонстрирует простейшую
векторную анимацию на БЕЙСИКе. Фигура 1 (рис.38) переходит в фигуру 2
(рис. 38) за несколько шагов, количество которых задано переменной
steps.
10 CLS: OVER 1: REM задавая режим OVER 1, мы
обеспечиваем стирание ранее нарисованного изображения путем повторной
печати в том же месте. Режим OVER 1 на БЕЙСИКе работа ет так же, как
наложение по X0R в машинном коде.
20 DIM а(10): REM массив описания сторон
30 DIM х(5): DIM у(5): REM массивы координат исходной фи
гуры
40 DIM р(5): DIM q(5): REM массивы координат вершин конечной фигуры
50 DIM d(5): DIM е(5): REM вспомогательные
массивы, в которых хранятся приращения координат х,у прн переходе от
точки N к вершине N+1. Нужен для команды DRAW.
60 FOR i=l ТО 5
70 READ x(i): READ y(i):REM Ввод координат вершин исходной
фигуры.
80 NEXT i
90 FOR i=l TO 5
100 READ p(i): READ q(i):REM Ввод координат вершин конечной
фигуры.
110 NEXT i
120 FOR i=l TO 10
130 READ a(i) :REM ввод описания сторон фигуры.
140 NEXT i
150 LET steps=10 :REM Можете поменять это число по
своему вкусу.
160 FOR k=l ТО steps
170 FOR j=l TO 5
180 LET x(j)-x(j)+(p(j) x(j))/steps*k
190 LET y(j)-y(j)+(q(j)y(j))/steps*k
200 NEXT j
210 GO SUB 500: PAUSE 50:REM Печать фигуры.
220 GO SUB 500 :REM Стирание фигуры.
230 NEXT k
240 OVER О :REM Восстановление режима перед
выходом
250 STOP
500 PLOT х(1),у(1) 510 FOR i=l ТО 5
520 LET d(i)=x(a(2*i))-x(a(2*i-l)) 530 LET e(i)=y(a(2*i))-y(a(2*i-l)) 540 DRAW d(i),e(i) 550 NEXT i 560 RETURN
|
900
|
DATA
|
128
|
,150
|
|
910
|
DATA
|
192
|
,100
|
|
920
|
DATA
|
168
|
,40
|
|
930
|
DATA
|
88,
|
40
|
|
940
|
DATA
|
64,
|
100
|
:REM координаты вершин исходной фигуры
|
1000
|
DATA
|
128
|
,150
|
|
1010
|
DATA
|
168
|
,40
|
|
1020
|
DATA
|
64,
|
100
|
|
1030
|
DATA
|
192
|
,100
|
|
1040
|
DATA
|
88,
|
40
|
|
1100
|
DATA
|
1,2
|
,2,3
|
:REM координаты вершин конечной фигуры
1100 DATA 1,2,2,3,3,4,4,5,5,1 :REM массив описания сторон