3.3.2 Преобразования координат внутри системы.
В ранках данного раздела мы будем обозначать
старые координаты символами X,Y,Z, а новые координаты со штрихом - X',
Y', Z' и т.п.
Преобразования плоской прямоугольной системы. Это самый
простой случай. Рассмотрим сначала параллельный перенос осей (см. рис.33).
Y"
Y
X' = X + Тх
У' = Y + Ту
Здесь Тх и Ту - координаты вектора, порождающего новую систему координат.
Рис. 33 Перенос осей
Поворот осей (см. рис. 34) на произвольный угол "teta" описывается следующей системой уравнений.
X' = X*COS(teta) - Y*SIN(teta)
Y' = X*SIN(teta) + Y*COS(teta)
Рис. 34 Поворот осей
Принцип композиции:
если происходит сложное перемещение, выражающееся одновременно в
изменении положения начала координат и в повороте координатных осей, то
итоговое перемещение можно рассматривать как результат двух независимых л
несвязанных между собой перемещений. То есть, пересчет кооэдинат можно
выполнять по частям, разбивая одно сложное преобразование на два или
более простых.
Таким образом, если нам надо одновременно повернуть оси и перенести их в новое место, то разбив задачу на две, мы получим :
X' = Тх + X»COS(teta) Y»SIN(teta) (7)
Y' = Ту + X*SIN(teta) + Y*COS(teta)
.Принцип композиции справедлив и для более
сложных преобразований : включающих в себя переводы из одних систем в
другие и внутрисистемные преобразования.
Преобразования полярной системы координат.
Согласно принципу композиции перемещений здесь мы также можем раздельно
рассмотреть перенос начала системы координат на радиус-вектор Т и
поворот координатной оси на угол "teta".
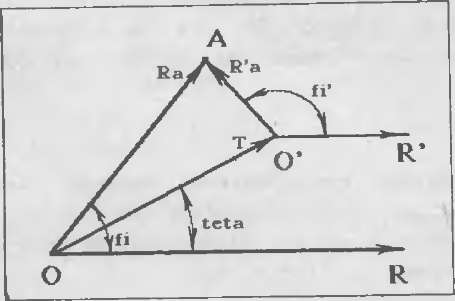
Рис. 35 Перенос начала полярной системы координат
Чтобы не путаться с векторами и обойтись без
аналитической геометрии, мы воспользуемся принципом композиции
перемещений и выполним эту операцию посредством нескольких
преобразований, например так:
переведем исходный вектор R в прямоугольную систему координат по формулам (2). обозначим эту операцию [Р1].
- переведем преобразующий вектор Т тоже в прямоугольную систему координат по тем же формулам (2). Это операция [Р2].
в прямоугольной системе координат перейдем от старых координат к новым по формулам (5). Пусть это будет операция [РЗ].
- вернемся к полярной системе координат по формулам (1). Пусть это будет операция [Р4].
Тогда вся операция переноса начала системы
координат (обозначим ее Т) будет представлять иэ себя как бы комбинацию
иэ более простых стандартных операций.
[Т] = {[Р1],[Р2],[РЗ],[Р4])
Вот тут-то нам бы очень пригодилась матричная
алгебра. Вы ведь видите, что иэ "кубиков" [Р1...Р4] мы "собрали"
операцию [Т], которая может быть "кубиком" для других, еще более
сложных операций.
Поворот координатной оси в полярной системе.
Эта задача совсем проста поскольку начало координат при этом не
меняется, то радиус-вектор остается тем же. А координатный угол
изменяется на величину поворота оси "teta".
R'=R
fi ' =f i+teta
Преобразования трехмерной прямоугольной системы координат.
На рис. 36 показан перенос осей в пространстве.
Ситуация здесь аналогично рассмотренной выше для плоской прямоугольной
системы и формулы для пересчета имеют следующий вид:
X1 = X + Тх
У = У + Ту (9)
Z' = Z + Tz
Здесь Тх, Ту и Tz - координаты вектора, порождающего новую систему координат.
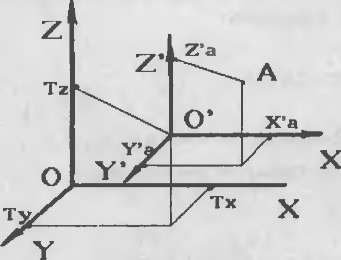
Рис. 36 Перенос осей в трехмерной прямоугольной системе координат
На рис.37 показан поворот координатных осей на угол "teta" вокруг оси X:
X' = X
У = Y*COS(teta) - Z*SIN(teta) (10)
Z' = Y*SIN(teta) + Z«COS(teta)
При повороте вокруг оси У:
X1 = X»COS(teta) + Z*SIN(teta) У = У (11)
Z' = -X*SIN(teta) + Z*C0S(teta)
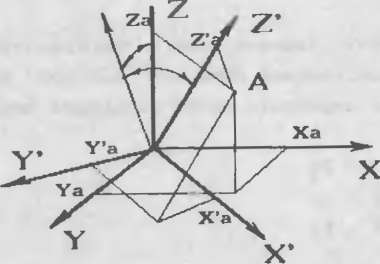
рис. 37 Поворот осей в трехмерной прямоугольной системе координат
При повороте вокруг оси Z:
X' = X*COS(teta) - Y*SIN(teta)
Y1 - X*SIN(teta) + Y*COS(teta) (12)
Z' = Z
Поворот вокруг некоей произвольной оси мы не
рассматрива ем, т.к. согласно принципу композиции перемещений можно
вместо него рассмотреть два поворота вокруг фиксированных осей и
результат будет тот же.
Преобразования сферической системы координат.
Чем дальше мы двигаемся, тем больше уравнений нам приходится выписывать
и, если мы захотим дать все необходимые уравнения для изменения начала
начала системы координат и для поворота радиуса-вектора, то получим
очень громоздкий раздел.
С другой стороны, на примере преобразования
полярной системы Вы, уважаемый читатель, уже поняли, что все можно
сделать более просто, если учесть принцип композиции перемещений.
- переводим сферические координаты исходного радиуса-вектора R в трехмерную прямоугольную систему по формулам (4);
- переводим сферические координаты преобразующего радиус-вектора R в ту же систему по тем же формулам (4);
- в новой системе по формулам (9-12) выполняем переносы и повороты осей;
- делаем обратное преобразование по формулам (3) и возвращаемся назад в сферическую систему координат.
3.4 Представление геометрических объектов в памяти компьютера.
3.4.1 Представление точки.
Это простейший геометрический объект. Для того,
чтобы описать точку, нам достаточно выделить несколько ячеек памяти (от
двух до шести) для хранения ее координат. Прежде всего, надо
определиться, в какой системе координат мы работаем. Если это плоская
система, то для задания точки достаточно двух координат, а если
пространственная, то нужно уже три
Теперь нам нужно определиться с тем, сколько
байтов мы расходуем на одну координату. Во многих случаях достаточно по
одному байту (от О до 255), но если этого диапазона значений Вам
недостаточно, то придется использовать по два байта (от О до 65535).
Какие координаты Вы запоминаете, зависит от
избранной системы координат Так, например, в трехмерной прямоугольной
системе Вы запоминаете, а впоследствии обрабатываете три проекции точки
на оси X,Y,Z. В сферической же системе координат Вы запоминаете длину
радиус-вектора и пару углов.