3.6 Проблемы линий невидимого контура.
Сокрытие линий невидимого контура - одна иэ
важнейших задач в компьютерной графике. Сразу оговоримся, что она имеет
множество решений. Самое общее решение - весьма сложное. Оно требует от
компьютера высокого быстродействия, а от программиста большого опыта и
потону мы его рассматривать не будем, а только наметим подходы, чтобы
те, кому это потребуется в реальной практике, знали с чего начинать.
Во втором томе нашей графической серии мы
рассмотрели один иэ возможных приемов сокрытия невидимых линий при
изображении сложной трехмерной поверхности. Метод довольно интересный
и, в определенной степени универсальный, но требующий большого объема
компьютерных вычислений. Для построения графиков и при обработке
результатов натурных или вычислительных экспериментов он подходит и
вполне соответствует задачам тома "Прикладная графика", но если мы
собираемся вести речь о графике динамической, то этот метод, увы, не
годится. Здесь нам нужна скорость. Мы даже согласны смириться с тем.
что само изображение может быть примитивным (например, космический
корабль из программы "ELITE"), но изображаться на экране оно должно не
только правильно, но и обязательно быстро.
По ходу игры корабль может совершать сложные
пространственные маневры, мы можем видеть его с разных сторон, но
всегда невидимые линии его контура не должны быть изображены. Проблема
состоит в том, что компьютер должен "решить сам", видика та или иная
линия или нет. Это интересная задача, которая предоставляет нашим
читателям широкие возможности для самостоятельных исследований, но с
чего-то надо начинать, и мы дадим здесь один несложный традиционный
алгоритм.
Давайте рассмотрим один иэ космических кораблей. Его проекции показаны на рис.42 Обратите внимание на то, что для то
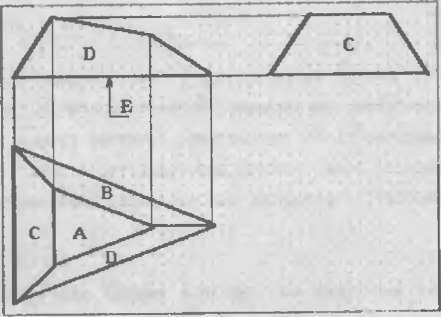
Рис. 42 Проекции "космического корабля"
го, чтобы изобразить на экране его трехмерное изображение (рис.43), нам было бы достаточно знать трехмерные координаты
его вершин (6 вершин по три байта), а также
условия связи их между собой, т.е. данные о том, какие вершины связаны
между собой, а какие нет (так, как мы это делали для плоского многоу
гольника) 9 ребер по 2 байта. Таким образом, для изображения этого
корабля в Рис. 43. "Космический корабль" любой его проекции нам бы
хватило всего лишь 36-ти байтов, которые можно задать один раз и всегда ими пользовать ся.
Тем не менее, в разделе, посвященном
представлению трех мерных тел, мы почему-то пошли по иному пути. Мы
представили каждый корабль не как набор вершин и связывающих их ребер,
а как набор плоских граней, каждая hj
которых имеет по нескольку плоских вершин. Для данного "корабля" у нас
получается 5 граней (A.B.C.D.E), иэ которых три грани -
четырехугольные, а две грани - треугольные.
Оказывается, такой подход может быть
использован для того, чтобы при произвольном положении космического
тела в пространстве, всегда можно было бы вычислить, какие грани
видимы, а какие - нет. И сделать это тоже очень просто - нам поможет
правило "часовой стрелки", которым мы руководствовались при нумерации
вершин.
Взгляните на рисунок 44 На нем видны две грани
нашего корабля - грань "А" и грань "Е". А теперь посмотрите, как
пронумерованы вершины при этих гранях. Если идти по этим вершинам в
порядке возрастания (А: 1.2,3), (Е: 4,5,6), то Вы увидите, что по грани
"А" обход совершается против часовой стрелки, а по грани "Е" наоборот -
по часовой стрелке. Интересно, не правда ли? Почему же так происходит?
А происходит это потому, что на грань "А" мы
смотрим как бы "снаружи", а на грань "Е" - как бы "изнутри". Вывод
однозначный -грань А - видима для нас и ее надо изображать, а грань "Е"
- невидима и ее изображать не надо. Такое решение принять очень прос то
и все это исследование по каждой грани можно поручить самому
компьютеру. Надо «только договориться, каким образом компьютер
узнает, что одна грань нумеруется против часовой стрелки, а другая - по
ней.
К счастью, и это тоже сделать нетрудно. Если у
Вас есть экранные координаты хотя бы трех вершин, принадлежащих данной
грани (а у Вас есть экранные координаты всех ее вершин), то дальше
логика простая. Возьмем любые три соседние
вершины, при надлежащие одной грани Запишем их координаты xl,yl: х2,у2;
хЗ,уЗ. Рассмотрим приращения координат х и у при переходе от точки
xl,yl к двум другим:
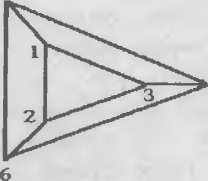
Рис. 44
Х2 XI
(IV)
уЗ yl
А теперь вспомним из школьного курса простую формулу для расчета определителя системы двух линейных уравнений:
Х2 - xl
(x3-xl)*(у2 yl)-(x2 xl)*(y3-yl) =
уЗ - yl
Так вот, если результат получится меньше нуля,
то это значит, что вершины пронумерованы "против часовой стрелки" и
изображать эту грань надо. Если бы результат оказался больше нуля, то
тогда вершины были бы пронумерованы "по часам", значит грань невидима и
изображению не подлежит.
Почему именно эта формула определяет, как
пронумерованы вершины, мы объяснять не будем Это доказательство входит
в курс аналитической геометрии и нам оно ни к чему. Если есть сомнения,
возьмите карандаш и бумажку в клеточку и через пять минут Вы убедитесь
в правильности формулы и сами.
Пример в машинных кодах мы приводить не будем.
Опытные "синклеристы" уже и так все поняли, и у них уже есть свои идеи
в голове, как применить этот алгоритм на практике. А для начи нающих мы
"повращаем" на экране космический корабль с помощью обыкновенного
БЕЙСИКа.
Возьмите лист бумаги в клетку и нарисуйте проекции нашего "корабля". За начало координат примем вершину 6 (0,0,0)
Всего вершин - 6, а граней - 5.
Тогда координаты вершин будут:
1 - (2,6,3) 2 - (2,2,3) 3 - (7,4,2)
4 - (0,8,0) 5 - (10,4,0) 6 - (0,0,0)
Теперь для всех пяти граней запишем условие обхода против часовой стрелки (если сиотреть на грань снаружи):
А - 1,2,3 В - 1,3,5,4 С - 1,4,6,2
D - 2,6,5,3 Е - 4,5,6
Вот мы и задали космический корабль. Можно
приступать к программированию, но когда будем описывать грани, введем
еще одно число - количество вершин в данной грани
Описание массивов:
массив трехмерных координат для всех вершин;
массив, описывающий грани против часовой стрелки; массив, в котором
хранится число вершин в каждой грани;
массив плоских (экранных) горизонтальных координат для каждой вершины;
w(6,3) -g(5,4) -р(5)
х(6)
У(6) -
массив плоских (экранных) вертикальных координат для каждой вершины
Демонстрационная программа
|
1
|
DIM
|
w(6.
|
3): DIM g(5,4): DIM p(5)
|
|
2
|
DIM
|
x(6)
|
: DIM y(6)
|
|
3
|
LET
|
teta
|
= PI/18: REM Шаг углового поворота
|
|
4
|
LET
|
st =
|
SIN (teta) LET ct = COS (teta)
|
|
5
|
LET
|
mx=2
|
: LET my=2 LET mz=2
|
|
6
|
LET
|
dmx
|
- 1: REM шаг приближения/удаления
|
10 DATA 6,5 REM количество вершин и граней 20 REM координаты вершин
21 DATA 2,6,3
22 DATA 2,2,3
23 DATA 7,4,2
24 DATA 0,8,0
25 DATA 10,4,0
26 DATA 0,0,0
30 REM описание граней (против часовой стрелки);
первое число - количество вершин в грани
31 DATA 3,1,2,3
32 DATA 4,1,3,5,4
33 DATA 4,1,4,6,2
34 DATA 4,2,6,5,3
35 DATA 3,4,5,6
40 REM ввод исходных данных 50 READ m,n
60 FOR k=l TO m : Ввод координат вершин 62 FOR j=l TO 3 64 READ w (k,j) 66 NEXT j: NEXT k
70 FOR k=l TO n: Ввод описания граней
72 READ p (k)
73 LET s = p(k)
74 FOR j=l TO s 76 READ g (k,j) 78 NEXT j: NEXT k
99 GO SUB 100: GO TO 300 100 REM пересчет трехмерных координат вершин
в двумерные экранные координаты по формулам для изометрической проекции (15)
105 CLS
110 FOR k = 1 ТО m
120 LET х(к) = mx*SQR(3)*(w(k,2)-w(k,1))/2 + 127 130 LET y(k) = my* (w(k, 3) (w(k, 2)+w(k, 1))/2 ) «• 87 140 NEXT к
200 REM решение вопроса о том, надо ли изображать
данную грань 210 FOR к = 1 ТО п
220 LET nl - g(k,l): LET n2 = д(к,2): LET пЗ = д(к,3):
REM взяли номера трех соседних вершин 230 LET
xl - x(nl): LET х2 = x(n2): LET хз - х(пЗ) 240 LET yl = y(nl): LET у2 =
y(n2): LET уЗ = у(пЗ) 250 LET test = (ХЗ-Х1)*(y2-yl)-(Х2-Х1)*(y3-yl)
260 IF test < О THEN GO SUB 1000: REM грань изображаем 270 NEXT к
280 RETURN
300 REM блок управления от клавиатуры
310 LET a$=INKEY$
320 IF a$="" THEN GO TO 300
|
330
|
IF
|
a$
|
=
|
к ^ и
|
THEN
|
GO
|
SUB
|
400:
|
REM
|
уменьшение
|
|
340
|
IF
|
a$
|
=
|
и 5 и
|
THEN
|
GO
|
SUB
|
500:
|
REM
|
крен влево
|
|
350
|
IF
|
a$
|
=
|
"6"
|
THEN
|
GO
|
SUB
|
600:
|
REM
|
тангаж
|
|
360
|
IF
|
a$
|
=
|
"7"
|
THEN
|
GO
|
SUB
|
700:
|
REM
|
тангаж
|
|
370
|
IF
|
a$
|
=
|
ngii
|
THEN
|
GO
|
SUB
|
800:
|
REM
|
крен вправо
|
|
380
|
IF
|
a$
|
=
|
"0"
|
THEN
|
GO
|
SUB
|
900:
|
REM
|
увеличение
|
|
390
|
IF
|
a$
|
=
|
,.q„
|
THEN
|
GO
|
SUB
|
9000
|
:REM
|
конец
|
399 GO TO 300
400 LET newmx=mx-dmx: IF newmx<l THEN RETURN 410 LET newmy=my-dmx
420 LET newmz=mz-dmx
440 LET mx=newmx: LET my=newmy: LET mz=newmz 450 GO SUB 100: REM рисуем новую картинку 460 RETURN
500 REM Вращение вокруг оси X против часов 520 FOR k=l ТО ш
530 LET у new = w(k,2)*ct - w(k,3)*st 540 LET znew = w(k,2)*st + w(k,3)*ct 550 LET w(k,2)=ynew: LET w(k,3)=znew 560 NEXT k
570 GO SUB 100: REM Рисуем новую картинку 580 RETURN
600 REM Вращение вокруг оси Y по часан 620 FOR k=l ТО ш
630 LET xnew = w(k,l)»ct - w(k,3)*st 640 LET znew = w(k,l)*st + w(k,3)*ct 650 LET w(k,l)=xnew: LET w(k,3)=znew 660 NEXT k
670 GO SUB 100: REM Рисуем новую картинку 680 RETURN
700 REM Вращение вокруг оси Y против часов
710 LET st=-st
720 GO SUB 600 :REM мы воспользуемся той же
процедурой, что и для вращения "по часам", только изменив синус угла
teta на противоположный. Косинус менять не надо, т.к. это функция
четная.
7 30 LET st=-st 740 RETURN
800 REM Вращение вокруг оси X по часам
810 LET st=-st
820 GO SUB 500
830 LET st=-st
840 RETURN
900 LET newmx=mx+dmx: IF newmx>10 THEN RETURN 910 LET newmy=my+dmx 920 LET newmz=mz+dmx
940 LET mx=newmx: LET my=newmy: LET mz=newmz 950 GO SUB 100: REM рисуем новую картинку 960 RETURN
1000 REM изображение грани
1020 LET s = p(k) : REM количество вершин в грани 1030 LET nf = g(k,l): REM номер первой вершины 1040 PLOT x(nf),y(nf)
1050 FOR f = 2 TO s : REM цикл по остальным вершинам
1060 LET nv = g(k,f): REM номер вершины 1070 LET dx=x(nv)-x(nf): LET dy=y(nv)-y(nf) 1080 DRAW dx.dy 1090 LET nf=nv 1100 NEXT f
1110 REM строим последнее (замыкающее) ребро к 1-ой вершине. 1120 LET nv=g(k,1)
1130 LET dx=x(nv)-x(nf): LET dy=y(nv)-y(nf) 1140 DRAW dx,dy 1150 RETURN