3.5 Плоское преобразование.
До
сих пор мы говорили о перемещениях и вращениях тел в пространстве, имея
в виду некоторые преобразования систем координат, которые являются как
бы "реальными", в которых эти объекты заданы, существуют и
взаимодействуют. Такие координаты называют "мировыми" или фактическими.
Но кроме них есть еще так называемые "наблюдаемые" координаты.
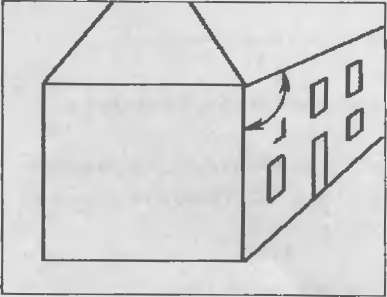
Рис. 40 Искажение углов при плоском преобразовании
Все, что Вас окружает в реальной жизни является
трехмерным, но попробуйте закрыть один глаз и Вы увидите только плоское
изображение окружающей действительности. Тем не менее Вы все равно
сможете отличить куб от сферы Тот факт, что "на глаз" угол между крышей
и углом соседнего дома равен 120-ти градусам (рис. 40) никак не введет
Вас в заблуждение. Всем своим жизненным опытом Вы подготовлены к тому,
что этот угол - прямой, а то, что он таковым не выглядит, так это
просто обман зрения.
"Наблюдаемые" координаты, как следует из их
названия, связаны еще и с наблюдателем. Понятно, что для наблюдателя
объект является как бы двумерным, плоским, поэтому для отыскания этих
наблюдаемых координат надо еще определиться с типом премирования
трехмерного тела на двумерную визуальную плоскость. Способы же такого
проектирования (типы) бывают разными.
Из курса черчения средней школы Вы знаете, что
наиболее часто применяется два типа аксонометрических проекций
трехмерных тел на плоскость - это диметрическая проекция и
изометрическая проекция. Они показаны на рис. 41.
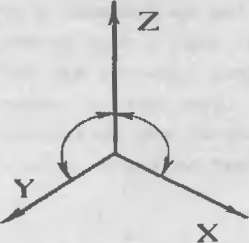
Рис. 41 Диметрическая и изометрическая проекция
Как видите, в диметрической проекции фиксируют
направления осей Y и Z, а ось X направляют под углом 135 градусов по
отношению к ним.
В изометрической проекции фиксируют направление
оси Z, а оси X и Y располагают так, чтобы между всеми осями
образовывался угол в 120 градусов.
Таким образом, при пересчете координат из
трехмерных фактических в наблюдаемые координаты на визуальной плоскости
важную роль играют углы наклона координатных осей "alfa" и "beta".
Для диметрической проекции мы получаем:
X1 = Y - X*COS(alfa) (13)
Y* = Z - X*SIN(alfa)
Поскольку угол "alfa" известен и равен 45 градусам, то получаем следующие формулы преобразования:
X' = Y - X*SQR(2)/2 (14)
Y1 = Z - X*SQR(2)/2
Для изометрической проекции мы получаем:
X' = Y*COS(beta) - X*COS(alfa) (15)
Y' = Z - X*SIN(alfa) - Y*SIN(beta)
Здесь углы "alfa" и "beta" тоже известны и равны 30 градусам . Таким образом:
X' = (Y-X)*SQR(3)/2 (16)
Y' = Z-(X+Y)/2
Если Вам из каких-то соображений захочется
использовать иные типы проекций с другими значениями углов "alfa" и
"beta", то Вы сами сможете рассчитать необходимые формулы, но при всех
условиях постарайтесь зафиксировать хотя бы одну ось. Принято всегда
фиксировать вертикальную ось, чтобы линии, являющиеся вертикальными в
трехмерном объекте, оставались вертикальными и в наблюдаемом
изображении, иначе изображение выглядит неестественно.