3.3 Координатные преобразования.
Это важная задача, причем она имеет отношение
не только и не столько к пересчету иэ полярной системы в плоскую
прямоугольную и наоборот или к пересчету иэ сферической системы в
прямоугольную трехмерную и т.п.. Дело в том, что очень часто приходится
делать преобразования, оставаясь в одной и той же системе, например при
изменении координат точки начала отсчета или при повороте координатных
осей. Так что задача разбивается на две: пересчет координат между
системами и преобразования систем координат.
3.3.1. Пересчет координат нежду системами.
Перевод координат иэ плоской прямоугольной системы в полярную показан на рис.31. Уравнения для пересчета очень просты:
Ra = SQRT (ха*ха + Ya*Ya) fi = arctg (Ya/Xa)
Y
Ya
Xa
Рис.31 Перевод координат из плоской прямоугольной системы в полярную
Перевод координат иэ полярной системы в плоскую прямоу гольную - это задача обратная к только что рассмотренной:
Ха = Ra*COS(fi) (2)
Уа = Ra*SIN(fi)
Перевод координат иэ прямоугольной трехмерной системы в сферическую показан на рис.32 Уравнения имеют вид:
R = SQRT (Ха*Ха + Уа*Уа + Za*Za)
psi = arctg (Za/SQRT(Xa*Xa + Уа*Уа)) (3)
fi = arctg (Ya/Xa)
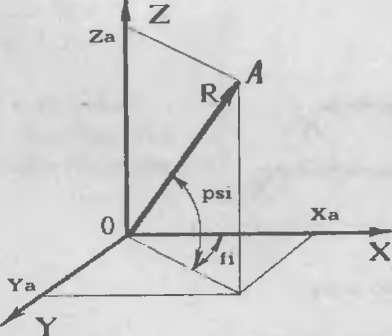
Рис. 32 Перевод координат из прямоугольной системы координат в сферическую.
Обратный перевод координат иэ сферической системы в прямоугольную описывается следующими уравнениями'
= R*COS(psi)*COS(fi) = R*COS(psi)«SIN(fi) - R*SIN(psi)