3. 3 Трехмерная векторная графика.
Здесь мы рассмотрим те приемы, которые служат для изобра-
жения трехмерных объектов на плоском экране телевизора или мо-
нитора.
Все тела, которые окружают нас в реальной жизни, являются
трехмерными, т. е. имеют длину, ширину и высоту. Космический
корабль "Таргонов". если вы его видели, тоже трехмерный, а вот
изображение его на Вашем экране всего лишь двумерное, посколь-
ку экран плоским. Так было и так будет по крайней мере до тех
пор, пока ученые не изобретут способ подключения к компьютеру
мониторов, создающих трехмерные изображения, например с помошью
голограФической техники, для нас же это означает то. что нам
надо научиться так изображать на плоском экране объемные тела,
чтобы создалась иллюзия, что они и на самом деле объемные. Та-
кая техника исполнения изображении и называется трехмерной гра-
фикой (3D-графикой). В основу изображения трехмерных тел поло-
жено проектирование координат их вершин на плоскость и соедине-
ние полученных точек между собой. Существует очень и очень
много способов получения проекций. Мы же здесь остановимся
только на одном.
Взгляните на Рис. 29. Здесь изображен куб.
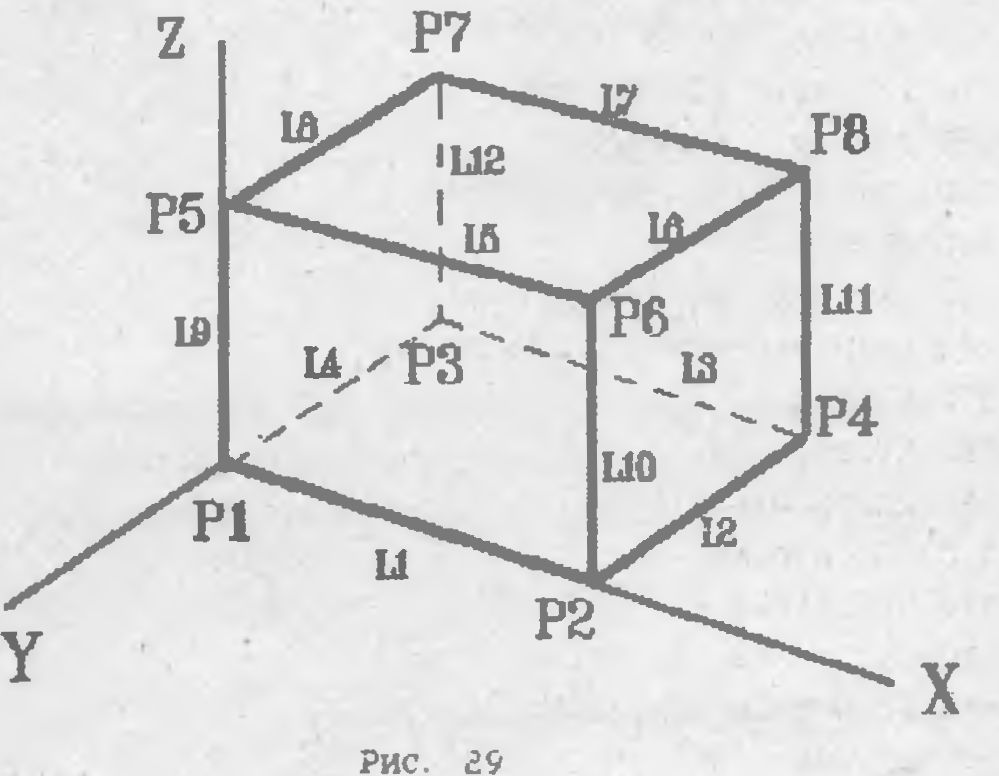
КУ6 имеет восемь вершин iPl, ..Р8) и, двенадцать ребер
(L1...L12). Ниже приведена программа на БЕИСИКе. которая нари-
сует такой куб на экране.
10 DIM Р(8. 3)
20 DIM W(12. 2)
30 FOR m=0 TO 1
40 FOR J=0 TO 1
50 FOR K=0 TO 1
60 LET P(4»m*2»J*K*l.1)=10»K
70 LET P(4«m+2«j*K+1.2)=10»j
60 LET P(4»m+2«J+K+1. 3) = 10»m
90 NEXT К
100 NEXT J
110 NEXT m
120 FOR m=l TO 12
130 FOR J=1 TO 2
140 READ W(m. J)
150 NEXT J
160 NEXT Ш
170 DATA 1.2.2.4.4. 3. 3. 1
160 DATA 5,6.6.8.6.7.7.5
190 DATA 1, 5. 2. 6.4. 6. 3. 7
200 FOR m=l TO 12
210 LET a=l: GO SUB 500
220 LET pi = 5«p*128
230 LET 41 = 5»q+66
240 PLOT P. 4
250 LET a=2: GO SUB 500
260 DRAW 5»p+126-p1. 5«q*86-ql
270 NEXT m
280 STOP
500 LET a=w(jn. a)
510 LET x=P(a,1)
520 LET y=p<a. 2)
530 LET Z=p(a. 3)
540 RANDOMIZE USR XXXXX
550 RETURN
He обращайте пока внимания на оператор RANDOMIZE USR в
строке 540. Сейчас пока он нас не интересует, и мы к нему еше
вернемся.
В строке ю задается массив ро. в котором хранятся коор-
динаты вершин. Его размерность в X 3, поскольку куб имеет в
вершин, а каждая вершина имеет три координаты. В строке 20 за-
дается массив wo. в котором хранятся ребра. Его размерность
12 X 2. поско1ьку у куба 12 ребер и каждое соединяет по две
вершины. Мы здесь экономим память, поскольку не храним в этом
нассиве координаты концов ребер (потребовался бы массив вдвое
больше), а храним только номера соединяемых вершин, благо их
координаты уже известны из массива ро. в строках 30... но ини-
циализируется массив координат вершин р<). а в строках 120...
190 - массив ребер wo. здесь приходится использовать массив
DATA, поскольку нет чисто вычислительного пути сделать так.
чтобы программа сама принимала решение о том. какие вершины
между собой соединены, а какие - нет.
Если Вы замените строки 60... 60 так. чтобы они заканчива-
лись на 8«к, 10»j, 12«ш. то получите уже не куб, а прямоуголь-
ный параллелепипед.
Теперь вернемся опять к основному нашему вопросу - как же
получается, что объемный куб у нас изображен на плоском экране?
Обратите, например, внимание на то, что ребро L7 у нас на экра-
не соединено с вершинами Р7 и Р8 несмотря на то. что это не сам
куб, а только его проекция на плоскость. Отсюда следует гене-
ральный вывод- если вершины тела соединены между собой отрезка-
ми прямых в пространстве, то проекции этих вершин на плоскость
тоже должны быть соединены на экране, вывод в обшем-то совер-
шенно очевидный, но пусть Вас не вводит эта очевидность в за-
блуждение. ведь именно в этом и состоит вся концепция изображе-
ния пространственных тел на плоском экране. По пространственным
координатам вершин найдите координаты их проекции на плоскость.
пользуясь математическим аппаратом из геометрии и тригонометрии
и соедините их между собой отрезками прямых, пользуясь процеду-
рой DRAW_LINE или с помошью технологии построения клиппирован-
ных отрезков, описанной выше - и все.
Остался открытым только один вопрос - а как найти плоские
координаты проекции вершины тела на плоскость? Это зависит от
того, какой метод проектирования мы примем. Как мы уже сказали.
существует очень и очень много разных видов проекции и Формулы
пересчета координат зависят от избранного вида. Очень хорошо
для этой задачи подходит так называемая изометрическая проек-
ция. Она характеризуется тем, что оси X. V и Z располагают на
экране под равными углами - 120 градусов <2«Р1/3) - см. Рис. 29л
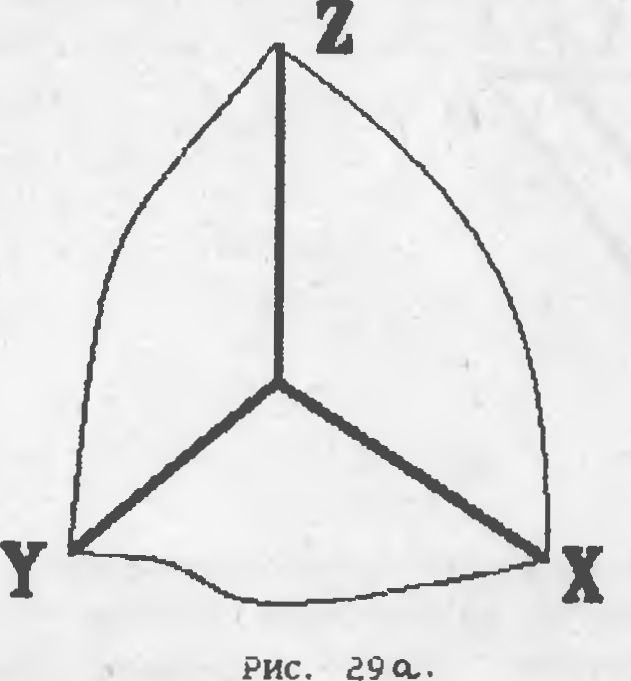
Формулы пересчета оказываются для этого вида проекции
очень простыми. Так, если вершина тела имела пространственные
координаты X. V, Z, то координаты ее проекции на плоскость Р и
О будут следующими:
LET P-SQR<3)*<У-Х)/2 (2)
LET 4=Z-lY+Xi/2
Итак, все оказалось просто и решается даже в БЕИСИКе.
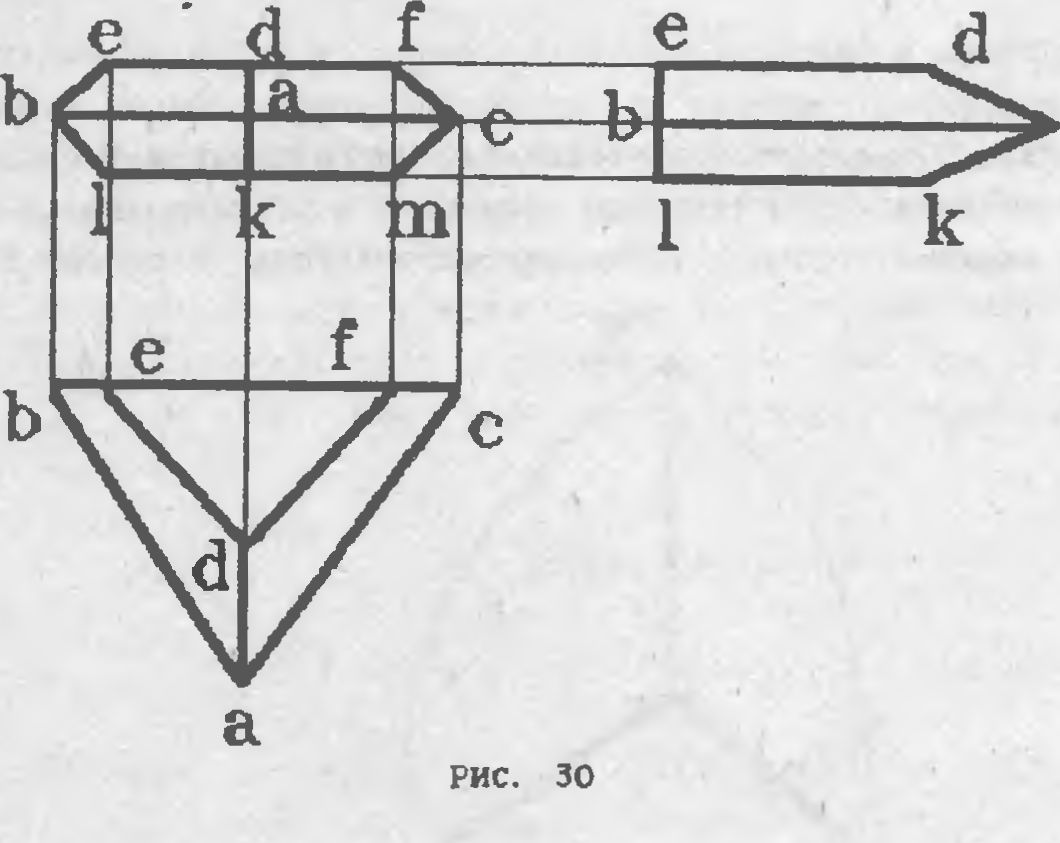
Возьмите миллиметровую бумагу, вычертите три вида своего объек-
та. на Рис. 30 мы взяли для примера полицейский корабль "Viper"
Из игры "ELITE". Пронумеруйте вершины, задайте трехмерные коор-
динаты каждой вершины и заполните массив вершин. Пронумеруйте
ребра и заполните массив ребер, указав какую пару вершин каждое
ребро соединяет. А теперь можете, пользуясь Формулами проектив-
ной связи (2) рассчитать плоские координаты каждой из вершин.
Теперь, если в Вашей программе предполагается приближение
или удаление от объекта, вы вспомните Формулы и) из предыдуше-
го раздела и пересчитаете плоские координаты объекта в экран-
ные. учитывая удаленность объекта от наблюдателя. Если при этом
какие-то вершины окажутся вне пределов экрана, Вам на помощь
придет технология клиппирования отрезков.
А тейерь вернемся к нашей БЕЙСИК-программе для изображения
прямоугольного параллелепипеда, там не решеи только один вопрос
- нет Формул проективной связи (2), но там есть вызов подпро-
граммы пользователя RANDOMISE USR ХХХХХ. Вот этим-то и занима-
ется эта подпрограмма. Конечно, можно было бы расчет этот сде-
лать и в БЕИСИКе. но БЕЙСИК не слишком быстро занимается мате-
матическими расчетами, поэтому эту подпрограмму мы оформили в
машинный код с привлечением кодов встроенного калькулятора.
Структурно подпрограмма состоит из трех частей. Первая
часть SEARCH.VAR нужна для того, чтобы была связь с головной
БЕЙСИК-программой и она служит для того, чтобы найти в области
переменных БЕИСйКа исходные координаты вершины. Вторая часть -
STK.ZYX - передает найденные координаты в калькулятор, а тре-
тья часть - TRANSFORM занимается непосредственно преобразовани-
ем координат по Формулам (2).
Увязка БЕИСИКа с малинным кодом и передача параметров от-
носится к задачам первостепенной важности. До сих пор мы пере-
давали параметры через FN о или через выделенные для этой пели
ячейки памяти, нижеприведенный алгоритм явится для бас отличной
школой того, как это делается через область программных пере-
менных. поскольку построен весьма рационально.
Процедура SEARCH.VAR
Код ' Нетка Мнемоника Комментарий
2А4В5С SEARCH.VAR LD HL,(VARS) ;HL указывает на область прог-
раммных переменных.
7Е S.V.LOOP LD A.(HL) .очередной байт из области пе-
; ременных.
E67F AND 7F ;Гасим старший бит.
37 SCF ; Включение флага переноса.
ее RET Z ; выход с включенным флагом пе-
;реноса, если найден код вон.
: т. е. достигнут конец области
;переменных, а переменная не
: найдена.
В9 CP С ;Сравнение найденной переменной
; с заданной в регистре С.
С8 RET Z ;Возврат с выключенным Флагом
.-переноса, если нужная перемен-
;ная найдена.
С5 PUSH ВС ;Запомнили имя искомой перемен-
;ной. ВС необходимо сохранить
; от порчи при работе вызываемой
; процедуры НЕХТ.ОНЕ.
CDB819 CALL 19В8Н :Вызов процедуры системного ПЗУ
I
; NEXT.OHE. которая найдет сле-
дующую переменную в области
; VARS и выставит ее адрес в DE.
ЕВ EX DE.HL ;Перенос этого адреса в HL.
Cl POP ВС ; Восстановили имя переменной.
lSFl JR S.V.LOOP ; возврат назад для продолжения
; поиска.
Процедура STK_ZYX
Код Нетка Ннемоника Комментарий
0е7а STK.ZYX LD С. 7АН : 7АН = 122 DEC - это код симво-
; ла z.
CD???? CALL GET.VAR ;значение переменной z перено-
;сится на стек калькулятора.
ОЕ79 STK.YX LD С.79Н ;79Н = 121 DEC - код "у".
CD???? CALL GET_VAR ;значение переменной у перено-
;сится на стек калькулятора.
0е78 LD С.76н ; 76н = 120 DEC - код "x".
CD???? GET.VAR CALL SEARCH.VAR; Поиск переменной в области
; программных переменных БЕИСИКа
DA2E1C JP С.1С2Е ;Если при выходе из SEARCH.VAR
.включен Флаг переноса, то зна-
; чит такая переменная не найде-
на и следует переход в ПЗУ иа
:процедуру REPORT.2. которая
; выдаст сообщение об ошибке
; "Variable not found".
23 INC HL ;Теперь HL указывает не на имя.
;а на значение переменной.
C3B433 JP ЗЗВ4Н ; Переход на процедуру ПЗУ
;STACK.NUM. которая перенесет
;число, на которое указывает
;регистровая пара HL на верши-
;иу стека калькулятора, она же
. выполнит возврат в вызывавшую
. процедуру.
Процедура TRANSFORM
Код Метка Мнемоника Комментарии (стек калькулятора)
CD???? TRANSFORM CALL STK.YX ; Помешаем Y и X на вершину
;стека калькулятора.
EF RST ген ;включение калькулятора.
03 subtract :Y-X
3440B00003 stK_data_3 ;Y-X.3
гв sqr ;Y-x.SQR(3)
04 multiply :SQR(3)«(Y-X)
A2 const.half ;SQR(3)«(Y-X).1/2
04 multiply ;SQR(3)«(Y-X)/2
36 endcaic
0E70 LD С. 70H ; 70H = 112 DEC - код "p".
CD???? CALL ASSIGN.VAR; Переменной. код которой нахо-
;дится в регистре с. присваива-
;ется значение, хранящееся на
;вершине стека калькулятора.
; р = SQR(3)*(у-Х)/2
CD???? CALL STK.ZYX ;Принимаем Z. Y и X на стек
; калькулятора.
EF RST 26Н ; Z. Y. X
OF add ;Z. Y+X
A2 const_haif ;Z. Y+X. 1/2
04 multiply ;Z. (Y+X)/2
03 subtract ;Z-(Y+X)/2
36 endcaic
0E71 LD С.71H ; 71H = 113 DEC - код "q".
CD???? ASSIGN.VAR CALL SEARCH.VAR
300A JR NC ASSIGN.VAR.2
C5 PUSH ВС ; запомнили код имени созда-
;ваемои переменной.
010600 LD ВС. 0006 : Подготовка к выделению до-
; полнительных шести ячеек
; памяти в области VARS.
CD5516 CALL 1655Н ; вызов процедуры ПЗУ MAKE-ROOM.
.которая вставит столько новых
;ячеек памяти, сколько указано
. в ВС. На место вставки указы-
; вает HL.
23 INC HL .HL указывает на первый байт
/ : выделенного пространства.
Cl POP ВС ;Вернули со стека код имени
;создаваемой переменной.
71 LD (HL).C ;Поместили его в область VARS.
23 ASSIGN.VAR.2 INC HL ; HL теперь указывает на место-
; положение числового значения
; создаваемой переменной.
Е5 PUSH HL
CDBF35 CALL 35BFH ; Вызов процедуры ПЗУ STK.PNTRS.
;По этой процедуре в HL выстав-
ляется адрес начала верхнего
; вложения на калькуляторном
; стеке.
22655С LD (STKEND), HL ; Изменяем значение tSTKEND).
Di POP DE ; DE теперь указывает на место-
; положение числового значения
; создаваемой переменной.
010500 LD ВС,0005 Подготовка к копированию
; пяти байтов из (HL) в (DE).
EDBO LDIR ;Перенос значения новой пере-
; менной со стека калькулятора
;в область VARS.
С9 RET