Камертон и музыкальный сопроцессор
© Рюмик С М., г. Чернигов, 1995.
Применение музыкальных сопроцессоров AY-3-8910/12 (в дальнейшем по тексту AY) по праву способствовало уникальному долголетию компьютеров ZX-Spectrum.
Музыкальные сопроцессоры появились в конце 1985 года в модели с расширенной памятью ZX-Spectrum-128 и затем присутствовали во всех последующих фирменных и отечественных разработках с памятью 128 и более Кб.
При всем разнообразии схем включения музыкальных сопроцессоров, один вопрос до сих пор решается неоднозначно, какой же должна быть частота, подаваемая на тактовый вход AY-микросхемы? В переводе фирменного описания указана цифра 1,7734 МГц с точностью 0,01% [1]. В реальных схемах частоту выбирают в диапазоне 1-2 МГц, рассчитывая услышать "именно те звуки, которые были задуманы при написании программы" [2].
Объяснить этот феномен, а также ответить на вопросы: какая же должна быть "истинная" частота и так ли был прав сэр Клайв Синклер, устанавливая определенные константы в ПЗУ-128, поможет предлагаемая публикация.
1. Общие сведения из теории музыкальной акустики.
Частоты акустических колебаний в пределах 20 - 20000 Гц называются звуковыми.
Высота звука - это качественная оценка частоты колебаний звука. С ростом частоты высота звука увеличивается.
Человеческое ухо чувствительно к изменению высоты тона более, чем к какому-либо другому параметру звука. Человек способен различить в диапазоне до 4000 Гц изменение частоты в 1 Гц. А по биениям частот двух тонов он может обнаружить разность частот до десятых долей Гц! [3].
Каждый звук в мелодии имеет свою частоту. Соответствие ноты и частоты звука подчиняется строгим математическим законам. В 1700 году немецкий ученый и музыкант Андреас Веркмейстер предложил математическую модель музыкальной шкалы, основанную на теории иррациональных чисел. Речь идет о логарифмически равномерной или, по-другому, равномерно темперированной музыкальной шкале, которой мы пользуемся и поныне.
Звукоряд насчитывает семь полных и две неполных октавы. Это (снизу - вверх): субконтроктава (три верхних звука), контроктава, большая октава, малая октава, первая, вторая, третья, четвертая октавы и пятая октава (три нижних звука). В октаве 12 нот, итого в звукоряде 90 нот, что соответствует клавиатуре пианино.
Нотный состав музыкальной шкалы приведен в таблице 1.
Таблица 1.
|
Нота |
до |
до-
диез |
ре |
ре-
диез |
ми |
фа |
фа-
диез |
соль |
соль-диез |
ля |
ля-
диез |
си |
|
Обозначение |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
# - знак повышения высоты тона на полтона.
Интервал между любыми двумя рядом расположенными нотами табл.1 называется полутоном.
Частоту любой ноты F(i) можно вычислить, зная частоту рядом стоящей ноты F(i-1), по формуле:
1
F (i) = 212* F (i -1) (1)
В качестве стандарта звукового и частотного соответствия принята нота "ля" первой октавы, имеющая частоту ровно 440 Гц. Недаром камертон (устройство, являющееся эталоном высоты звука) воспроизводит именно 440 Гц.
Все остальные 11 нот октавы являются производными от "ля" и не имеют абсолютно точного значения частоты, так как число "корень двенадцатой степени из двух" в формуле (1) является иррациональным, то есть приближенным (=1,05946...).
Цент - это единица частотного интервала, равная 1/100 полутона. Октава равна 12 полутонам или 1200 центам.
2. Структурная схема музыкального сопроцессора.
Музыкальный сопроцессор в справочнике [4] назван программируемым генератором звуков. По принципу работы он наиболее близок к классу музыкальных синтезаторов.
Основой любого электромузыкального инструмента (ЭМИ) является генераторный блок, который, как известно [5], выполняют либо с 12 отдельными тональными генераторами, либо с одним, работающим совместно с делителями частоты. Именно второй способ применен в архитектуре AY.
На рисунке 1 приведена структурная схема музыкального сопроцессора [4]. Для упрощения анализа в структуре оставлены только элементы, влияющие на высоту звука, форма сигнала и спецэффекты не рассматриваются.

Рис.1.
Управление генераторами тона A, B, C, осуществляется через 6 внутренних управляющих регистров R0-R5. Каждый канал снабжен собственным программируемым счетчиком. Выходная частота получается делением синхронизирующей тактовой частоты CLK сначала на КСЧ=16 с последующим делением полученного результата на 12-разрядную величину, соответствующую частоте тона.
Значение 12-разрядной величины получается путем комбинации содержимого 4 младших разрядов грубого тона (R1, R3, R5 - число 0-15) и 8 разрядов регистра точного тона (R0, R2, R4 -число 0-255).
Все три канала A, B, C, работают независимо друг от друга.
3. Программирование музыкального сопроцессора.
С точки зрения программиста музыкальный сопроцессор в Спектруме представляет собой устройство, имеющее два порта: выходной порт с адресом #BFFD (49149) и входной/выходной порт с адресом #FFFD (65533).
Из 16 внутренних регистров AY в установке высоты тона участвуют шесть: R0-R5.
Для работы с регистрами первоначально в порт #FFFD заносится его порядковый номер, для R0 это #00, R1 - #01, R2 - #02 и т.д. Затем в порт #BFFD заносится конкретное число, определяющее в случае регистров R0-R5 коэффициент деления входной частоты.
Программирование высоты тона музыкального сопроцессора осуществляется следующими способами:
- через оператор вывода OUT на БЕЙСИКЕ-48 или БЕЙСИКЕ-128;
- через команду АССЕМБЛЕРА OUT в машинных кодах;
- через оператор PLAY на БЕЙСИКЕ-128.
Команда PLAY гораздо более гибкая, чем обыкновенный BEEP, так как позволяет программировать мелодию непосредственно в нотах выбранной октавы. Формат команды PLAY при воспроизведении, например, камертонной ноты "ля" первой октавы:
PLAY "О4А"
где цифра "4" после заглавной буквы "О" обозначает порядковый номер октавы, а заглавная буква "А" является символом ноты "ля".
Оператор PLAY охватывает 9 октав, число после буквы "О" может изменяться только в пределах от 0 (субконтроктава) до 8 (пятая октава). Действительно, задайте: PLAY "O9A", и получите ошибку: "Out of range".
Буква, обозначающая ноту, может быть как заглавная ("А"), так и строчная ("а"), причем строчная буква обозначает понижение одноименной ноты ровно на октаву.
Коэффициенты деления оператора PLAY зашиты в ПЗУ-0 (ПЗУ Спектрум-128) и занимают область 216 байтов по адресам #1096-#116D.
4. Определение коэффициентов деления и частоты CLK.
Из трёх способов программирования звука только последний, через оператор PLAY, даёт абсолютный результат, то есть, имеется привязка к конкретным нотам. Это означает, что, запрограммировав звучание ноты "ля" первой октавы через команду PLAY и сравнив полученную частоту камертона, следует ожидать одинаковые результаты.
Так как высота ноты для Спектрума однозначно зависит от тактовой частоты, подаваемой на вход CLK сопроцессора, то идеальное звучание одной ноты возможно только для одной, вполне определенной частоты CLK.
Поиск частоты можно провести двумя путями.
Первый способ, практический. Подключить к входу CLK внешний задающий генератор в диапазоне 1-2 МГц и, изменяя его частоту, добиться совпадения звучания с эталоном. Способ сложен в реализации, так как измерение надо произвести для всех 90 нот звукоряда.
Второй способ, теоретический. Рассчитать требуемое значение частоты CLK, используя зашитые в ПЗУ компьютера Спектрум-128 коэффициенты деления. Этот способ предпочтительнее, так как позволяет при высокой точности результата провести математическую обработку.
Для нахождения коэффициентов деления можно использовать тот факт, что после выполнения команды PLAY в регистрах грубой и точной установки высоты тона остаются коэффициенты, которые можно прочитать, обратившись к порту #FFFD. Значение общего десятичного коэффициента деления Ki определится по формуле:
Ki = T + 256 * Gt (2)
где Ti и Gi - соответственно десятичные коэффициенты деления точного и грубого регистров для i-й ноты.
Частоту i-й ноты F(i) можно определить по формуле (1), зная эталонную частоту. Представим формулу (1) в удобном для вычисления виде:
F -
F (i) = * 212 (3)
16
где: Fля/16 - частота самой низкой ноты звукоряда F1, которая ровно в 16 раз меньше частоты эталона Fля=440 Гц;
i - от 1 до 90 - порядковый номер ноты.
Частотный диапазон исследуемого звукоряда F1-F90 равен 27,5-4698,6 Гц. Частота CLK i-й ноты определится по формуле:
CLK, = F(i)* K * Kcч (4)
где КСЧ=16 - коэффициент счёта общего для трех каналов делителя, находящегося внутри AY (рис.1).
Очевидно, что для каждой из 90 нот существует своя "истинная" CLK, то есть частота, при которой конкретная нота будет звучать абсолютно точно. Итого 90 частот CLK, которые можно вычислить, используя программу листинга 1.
Листинг 1. 10 REM AY-3-8910/12
20 LET I=0: LET R=65533: FOR N=1 TO 8 30 FOR M=1 TO 23 STEP 2 40 IF M=7 THEN LET N=N+1
50 LET A$="O"+"012345678"(N)+"N10"+" A#A B C#C D#D E F#F G#G"(M TO M+1) 60 PLAY A$
70 OUT R,0: LET T=IN R: OUT R,1: LET G=IN R
80 IF T=255 OR G=255 THEN GO TO 70
90 LET I=I+1: LET K=T+256*G
100 LET F=440/16*2A((I-1)/12)
110 LET CLK=F*K*16
120 IF I>90 THEN STOP
130 PRINT A$( TO 2);A$(6 TO );"F";I;" K=";K;" CLK=";CLK;" Hz" 140 NEXT M: LET N=N-1: NEXT N
Результат работы удобно представить в виде гистограммы (рис.2). Гистограмма - это график, по горизонтальной оси которого отложена исследуемая величина (в данном случае это CLK), а по вертикальной оси - частота ее повторения при выборке из ограниченного количества испытаний (в данном случае из 90 "истинных" CLK).
На гистограмме можно выделить рабочую зону, где находится 80 нот или 89% всех значений, две свободные зоны и две области "фальшивых" нот, имеющих предельно большой разброс CLK. Наибольшее число "попаданий" приходится на диапазон 1773000 - 1774000 Гц (31 значение или 34%), следовательно здесь и должна быть расчетная CLK.
5. Определение логически обоснованной частоты CLK.
Листинг 1 помог вычислить 90 значений CLK. Но в реальности частота CLK одна для всех нот, поэтому каждая нота будет звучать чуть-чуть "не так", с погрешностью.
Коэффициенты деления Ki, зашитые в ПЗУ 128К, были по какой-то методике заранее рассчитаны программистами сэра Клайва Синклера. Не зная этой методики, можно пойти от обратного - при известных коэффициентах деления вычислить пределы логически обоснованной частоты CLK.
Например, коэффициент деления для ноты F1 "ля" субконтроктавы равен 4031, именно 4031, а не 4030 или 4032. Поэтому можно вычислить три частоты CLK: CLK0 = 27.5 Гц * 4031 * 16 = 1773640 Гц CLKmin = 27.5 Гц * 4030 * 16 = 1773200 Гц CLKmax = 27.5 Гц * 4032 * 16 = 1774080 Гц Расположим полученные частоты на оси, как показано на рис.3. Логически обоснованным интервалом будем называть интервал между частотами MIN и MAX, определяемых из условия равенства логарифмов отношений частот:
MINi = Fi * KCT*SQR(Ki*(Ki-1)) = 1773420 Гц (для F1) MAXi = Fi * ^ч *S QR(Ki *(Ki+1)) = 1773860 Гц (для F1) где SQR - математическая функция "квадратный корень".
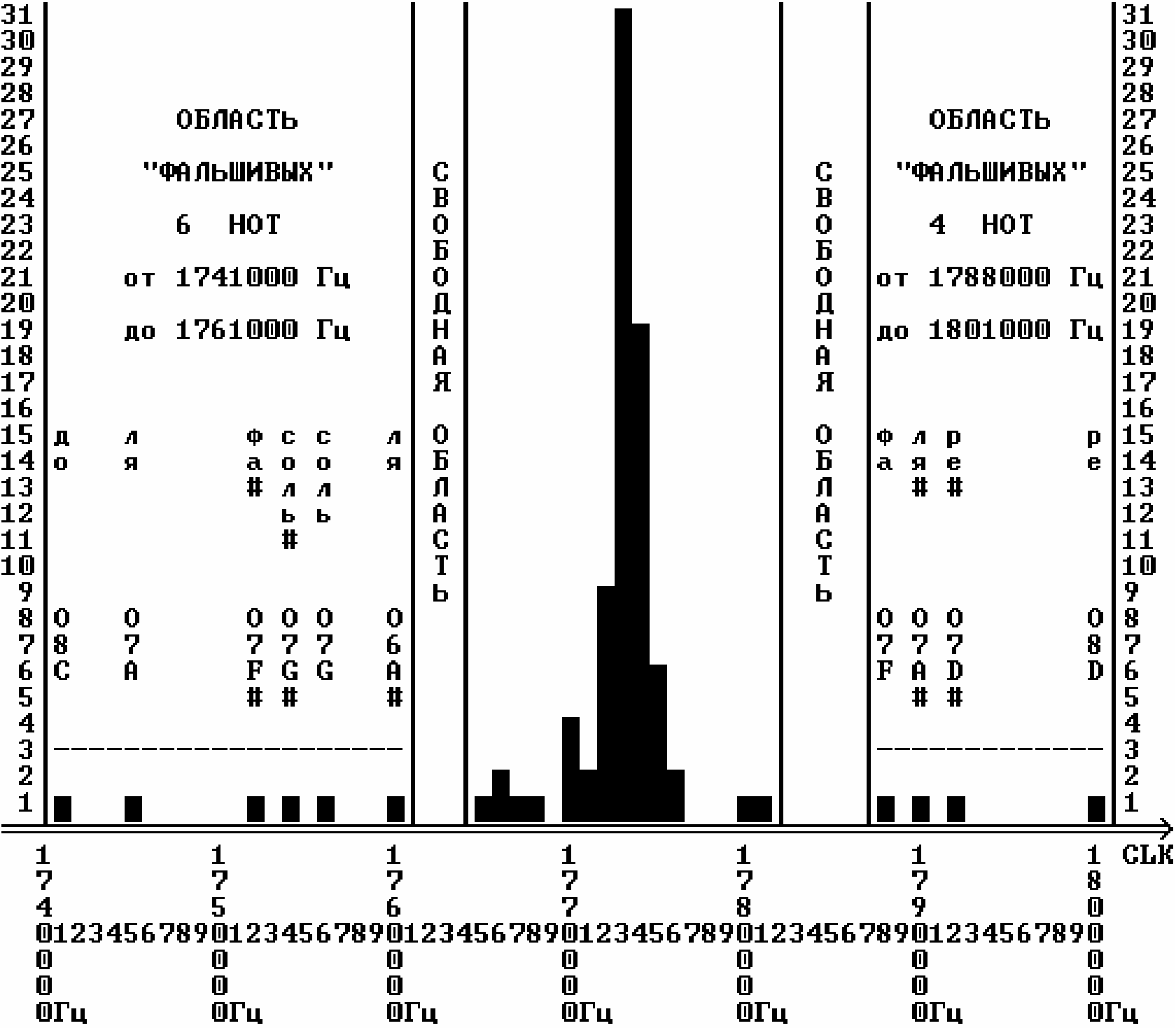
Рис. 2.
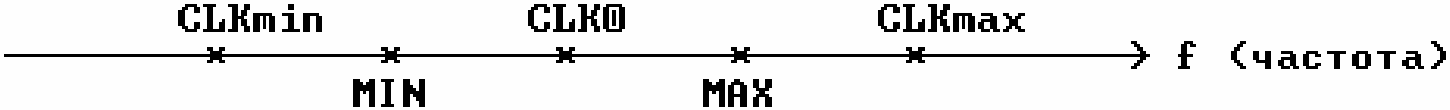
Рис. 3.
Приведенный пример рассчитан на самую низкую ноту, для которой логический интервал CLK самый минимальный. Поэтому можно утверждать, что, если коэффициент K1 выбран продуманно, а не произвольно, то "истинная" CLK находится в пределах MIN-MAX, иначе был бы выбран другой коэффициент. Аналогично для всех 90 нот можно вычислить интервалы MINi-MAXi, совместить их друг с другом на оси частот и посмотреть, какой же интервал, в конце концов, останется общим для всех.
Вычисления можно поручить компьютеру, дополнив при помощи команды MERGE листинг 1 строками из листинга 2.
Листинг 2.
10 LET e=1E-7: LET min=e: LET max=1/e 120 IF I<91 THEN GO TO 150
130 PRINT "MIN=";min;" Hz MAX=";max;" Hz": STOP 150 LET mi=F*16*SQR (K*(K-1)) 160 LET ma=F*16*SQR (K*(K+1))
170 IF mi-max>e OR min-ma>e THEN PRINT "ERROR F";I,"K=";K: GO TO 140
180 IF mi-min>e THEN LET min=mi 190 IF max-ma>e THEN LET max=ma 200 GO TO 140
Результат работы заставляет задуматься, общий интервал для 90 нот: MIN=1773441,5 Гц MAX=1773520 Гц
ошибочная нота "ре-диез" малой октавы (F31, октава 03). Если изменить ошибочный коэффициент K31=712 на 713, то интервал MIN-MAX останется прежним, а ошибка исчезнет.
Известны исследования однотипной ситуации для ЭМИ [5], показывающие, что в ряду коэффициентов деления существуют "магические" числа, которые позволяют свести к минимуму погрешности нот для вполне определенных входных частот.
Оказывается, что и для имеющегося ряда коэффициентов деления существуют другие комбинации чисел, при которых интервал MIN-MAX находится в главном пике гистограммы и отсутствуют ошибочные коэффициенты (таблица 2).
_Таблица 2.
|
КОЭФФИЦИЕНТЫ |
K1 |
K6 |
K17 |
K31 |
MIN MAX, Гц |
dF, Гц |
|
без коррекции |
4031 |
3020 |
1600 |
712 |
1773441-1773520 |
ERR.F31 |
|
K31 |
4031 |
3020 |
1600 |
713 |
1773441-1773520 |
79 |
|
K6 |
4031 |
3019 |
1600 |
712 |
1773420-1773423 |
3 |
|
K6, K31 |
4031 |
3019 |
1600 |
713 |
1773423-1773441 |
18 |
|
K1, K6 |
4030 |
3019 |
1600 |
712 |
1773414-1773420 |
6 |
|
K1, K6, K17 |
4030 |
3019 |
1599 |
712 |
1773395-1773414 |
19 |
Из таблицы 2 видно, что наиболее широкий интервал dF=MAX-MIN имеет вариант с коррекцией K31 для частоты F31. Думается, что при расчете коэффициентов ПЗУ-128 программистами сэра Клайва Синклера проводилась подобная оптимизация, однако коэффициент K31 был упущен из виду.
Необходимость в как можно более широком интервале dF очевидна.
На вход CLK поступает кварцованная частота. Точность настройки современных кварцевых резонаторов 1-20 МГц колеблется от (±5 - ±15)*1Е-6 для вакуумных резонаторов и до (±10 - ±50)*1Е-6 для обычных герметизированных. Здесь и далее "1Е-6" - число "десять в минус шестой степени".
В пересчете на частоту 1,77 МГц допустимые отклонения составят от ±8 до ±88 Гц.
Следовательно, расчетной следует признать частоту CLK = (1773480±40) Гц при точности настройки кварцевого резонатора не хуже ±20*1Е-6. Коэффициент K31 должен быть увеличен до 713.
6. Распределение абсолютных погрешностей нот.
Введем понятие абсолютной погрешности звучания ноты. Это та величина, на которую отличается звучание "идеальной" ноты (1) от реальной.
Малые музыкальные интервалы удобно измерять в центах, абсолютная погрешность i-той ноты определяется по формуле:
(5)
Si - абсолютная погрешность, в центах; Fi - реальная частота ноты; Fi(0) - "идеальная" частота ноты.
Задача состоит в том, чтобы для дискретных частот CLK из рабочей зоны гистограммы рис. 2 вычислить массив из 90 значений погрешностей |Si| и проанализировать результат методом "срезов". "Срез" - это в данном случае определенный уровень погрешности в центах.
где
Стандартного ряда для "срезов" не существует, поэтому можно воспользоваться косвенными сведениями: "1 цент" - это погрешность прибора для настройки музыкальных инструментов; "3 цента" - минимальная погрешность, которую способен различить человек на слух [3]; "5 центов" -максимальная погрешность установки частоты тона ЭМИ [6]; "10, 20 центов" - произвольно взятые целочисленные значения грубых погрешностей.
Программа на БЕЙСИКЕ, производящая вычисления массивов погрешностей по "срезам", получается, если добавить через MERGE строки из листинга 3 в листинг 1.
Листинг 3.
10 DIM C(90): LET e=1E-7
120 IF I>90 THEN GO TO 140
130 LET C(I)=CLK
150 FOR Z=1 TO 12 STEP 2
160 IF Z=7 THEN LET Z=10
170 IF Z=12 THEN LET Z=20
180 FOR C=1770000 TO 1778000 STEP 500
190 LET CENT=0: FOR I=1 TO 90
200 LET S=ABS (1200/LN 2*LN (C/C(I)))
210 IF Z-S>e THEN LET CENT=CENT+1
220 NEXT I
230 PRINT "CENT<";Z;" L=";INT (CENT*100/90+0.5);"% CLK=";C;" Hz" 240 NEXT C: NEXT Z
Результаты работы программы выводятся в форме: CENT<1 L=4% CLK=1770000 Hz. Это означает, что для частоты CLK равной 1770000 Гц из 90 нот 4% имеют абсолютную погрешность звучания менее 1 цента.
Для наглядности полученные результаты приведены в таблице 3.
Таблица 3.
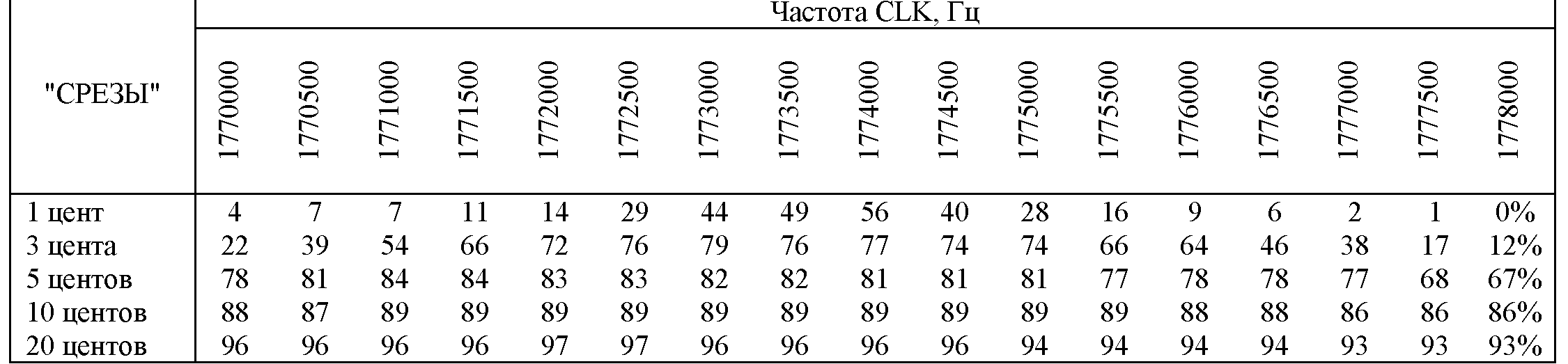
Как видно, расчетная частота CLK=1773480 Гц с точки зрения минимума абсолютных погрешностей не является оптимальной! И, вообще, говорить об оптимальной частоте можно только для конкретных "срезов".
Например, чтобы иметь максимальный процент нот, удовлетворяющих требованиям ЭМИ (5 центов), частота CLK должна быть в пределах 1771000 - 1771500 Гц и т.д.
Усредняя результаты таблицы 2, можно расширить диапазон допусти мой частоты CLK до 1771500 - 1775000 Гц, при этом снимаются жесткие ограничения на точность настройки кварцевого резонатора.
Разумеется, в фирменном ZXSpectrum-128 возможности варьировать частотой CLK не было, поскольку вся схема жестко привязана к одному кварцевому генератору.
7. Расчёт относительных погрешностей музыкальных интервалов.
Кроме абсолютных погрешностей, указывающих, на сколько отличаются ноты от "истинных" по частоте, не менее важны относительные погрешности музыкальных интервалов.
Музыкальная мелодия описывается последовательными интервалами между составляющими ее тонами. Для музыкального интервала характерно определенное отношение частот звуков. Именно отношение частот между звуками мелодии делают её узнаваемой.
Например, перенести мелодию выше - это значит воспроизвести её иными звуками (более высокими по частоте), но с точным сохранением отношений частот тонов в каждом интервале. Характер мелодии при этом на слух не искажается.
Можно выделить 12 основных музыкальных интервалов в пределах октавы [7]: от малой секунды (1 полутон) до октавы (12 полутонов).
Рассчитать, насколько фальшиво будут звучать все 12 интервалов в пределах полного звукоряда из 90 нот поможет формула (6). Формула расчёта не будет иметь зависимости от частоты CLK, так как сравниваются отношения частот, зависящие только от коэффициентов деления.
Г к Л
|dS(i,x)| = 1200*log2 —--100* x (6)
V —i+x J
где х от 1 до 12 - количество полутонов в музыкальном интервале; i от 1 до (90-х) - порядковый номер ноты.
Вычисления относительных погрешностей по формуле (6) можно выполнить, присоединив через MERGE листинг 4 к листингу 3. Результаты вычислений приведены в таблице 4.
Листинг 4.
130 LET C(I)=K 180 FOR X=1 TO 12
200 LET S=ABS (1200/LN 2*LN (C(I)/C(I+X))-100*X) 215 IF I+X=90 THEN GO TO 230
230 PRINT "CENT<";Z;" L=";INT (CENT*100/I+0.5);"% MUZ=";X 240 NEXT X: NEXT Z
Таблица 4.
|
"СРЕЗЫ" |
МУЗЫКАЛЬНЫЕ ИНТЕРВАЛЫ (количество полутонов) |
-Есред. |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 цент |
49 |
45 |
47 |
47 |
39 |
39 |
39 |
48 |
40 |
39 |
47 |
63% |
45.2% |
|
3 цента |
66 |
58 |
70 |
69 |
67 |
65 |
71 |
72 |
73 |
59 |
65 |
76% |
67.6% |
|
5 центов |
76 |
76 |
79 |
74 |
72 |
74 |
76 |
76 |
81 |
76 |
73 |
78% |
75.9% |
|
10 центов |
88 |
88 |
85 |
85 |
87 |
82 |
87 |
87 |
89 |
89 |
86 |
83% |
86.3% |
|
20 центов |
93 |
93 |
93 |
94 |
94 |
96 |
94 |
93 |
96 |
94 |
96 |
90% |
93.8% |
Распределение по "срезам" музыкальных интервалов достаточно равномерно. В среднем чуть более точно будут звучать октавы (х=12), чуть менее точно - малые септимы (х=10), чистые кварты (х=5).
Примерно третью часть всех интервалов в звукоряде человек с музыкальным слухом отнесёт к фальшивым ("срез" 3 цента). Кроме того, имеется около 7% очень грубых ошибок более 20 центов. Очевидно, что признать музыкальный сопроцессор эталонным источником звука для полного звукоряда нельзя.
Как показано [5], для известного максимального коэффициента деления (K1=4031) существуют оптимальные коэффициенты Ki(opt), которые минимизируют относительные погрешности:
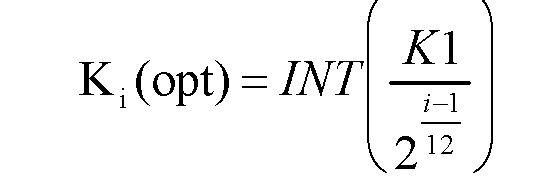
Где INT - функция округления до ближайшего целого числа.
Можно добавить через MERGE строки из листинга 5 в листинг 1 и сравнить оптимальные коэффициенты с имеющимися в ZX-Spectrum-128.
Листинг 5.
120 IF I=1 THEN LET K1=K 130 IF I<91 THEN GO TO 160 150 STOP
160 LET Kopt=INT (0.5+K1/2A((I-1)/12))
170 IF Kopt<>K THEN PRINT "ERROR F";I;" K=";K;" K(opt)=";Kopt 180 GO TO 140
Результат указывает на пять неоптимальных нот. Должно быть K2=3805, K4=3390, K13=2016, K15=1796, K31=713.
Если провести расчет погрешностей музыкальных интервалов по формуле (6) для оптимальных коэффициентов, то выяснится, что это отразится только на улучшении параметров по "срезу" 1 цент - было Lср=45.2%, стало Lср=46.5%. Следовательно, коэффициенты деления, зашитые в ПЗУ-128, близки к оптимальным.
8. Выводы.
1. Музыкальные сопроцессоры AY-3-8910/12 не предназначены для эталонного воспроизведения звука в широком диапазоне частот. При допустимой частоте CLK=1-2 МГц [4] эквивалентная частота генераторного блока составит всего 62-125 кГц вследствие деление частоты на 16 внутри музыкального сопроцессора (рис.1).
Отсюда низкие значения коэффициентов деления на высоких частотах (К90=24) и большая максимальная погрешность округления [5]: d=0.5/K90*100%=2,1%.
2. Расчётное значение частоты CLK для ZX-Spectrum-128 равно 1773480 Гц с точностью +20*1Е-6, при этом коэффициент К31 следовало бы увеличить на единицу. К31=713, ячейка #10D2 в ПЗУ-0: имеется #C8, должно быть #C9.
Однако на практике улучшение звучания ноты F31 для расчётной частоты CLK составит всего 0,05 цента, что можно зафиксировать лишь точными измерительными приборами. Поэтому перешивать ПЗУ128 сэра Клайва Синклера торопиться не надо во избежание головной боли от возможных проблем несовместимости ПЗУ.
При проектировании новых систем с музыкальными сопроцессорами следует проводить предварительное математическое моделирование с целью определения оптимальных коэффициентов деления.
3. Наиболее точно для музыкального сопроцессора звучат самые низкие ноты звукоряда, наиболее фальшиво - самые верхние. Абсолютные погрешности звучания нот для CLK=1773480 Гц приведены в таблице 5.
Таблица 5.
|
ОКТАВА |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
|
ЦЕНТЫ |
<0.2 |
<0.4 |
<0.7 |
<1.6 |
<3.3 |
<5.8 |
<12.9 |
<27.1 |
<31.6 |
Использовать в музыкальных произведениях ноты четвертой (07) и пятой (08) октав нецелесообразно, так как даже неискушенный слушатель заметит фальшь. На гистограмме рис. 2 перечислены 10 "фальшивых" нот, которые явно не рекомендуется применять.
4. При введении отдельного кварцевого генератора для частоты CLK можно получить результирующие абсолютные погрешности нот лучше, чем на фирменном ZX-Spectrum-128. Значение
оптимальной частоты выбирается по данным табл.3 в диапазоне 1771500 - 1775000 Гц. Схема подключения отдельного генератора может быть выполнена по аналогии с приведенной в [1], при этом следует изменить коэффициент деления счётчика K^ согласно таблице 6.
Таблица 6.
|
№ |
КВАРЦЕВЫЙ резонатор |
ТОЧНОСТЬ НАСТРОЙКИ |
Кцел |
РАСЧЁТНАЯ CLK |
|
1 |
РК169МВ-8ВТ-12399,5 кГц |
+30*1Е-6 |
7 |
1771357 Гц |
|
2 |
РК172-ТВ-1-8862,9 кГц |
+15*1Е-6 |
5 |
1772580 Гц |
|
3 |
РК100-4 АЛ-8866,99 кГц |
+5*1Е-6 |
5 |
1773398 Гц |
|
4 |
РК100-4 АЛ-8867,24 кГц |
+5*1Е-6 |
5 |
1773448 Гц |
|
5 |
РК 100-4БН-12425 кГц |
+5*1Е-6 |
7 |
1775000 Гц |
|
6 |
РК100-4АЛ-17734,47 кГц |
+5*1Е-6 |
10 |
1773447 Гц |
5. Если значение CLK будет находиться вне рабочей зоны рис. 2, то вместо абсолютных погрешностей, которые и так будут велики, следует обратить внимание на относительные погрешности, которые определяют узнаваемость мелодии.
Для получения минимальных относительных погрешностей музыкальных интервалов следовало бы изменить значения коэффициентов деления K2, K4, K13, K15, K31. Соответственно перешить ячейки ПЗУ-0: #1098 с #DC на #DD; #109C с #3D на #3E; #10AE с #DF на #E0; #10B2 c #03 на #04; #10D2 c #C8 на #C9.
Однако улучшения на слух не будет заметно, так как изменения коснутся только "среза" в 1 цент. Кроме того, ноты F2 - F15 редко используются на практике.
При желании все-таки изменить коэффициенты в ПЗУ-128 и иметь более точное звучание музыкальных интервалов, лучше сделать это через замещающее "теневое" ПЗУ.
6. Если тактовая частота CLK равна 1 МГц, то AY-мелодия будет звучать ниже по высоте почти на октаву (10 полутонов).
Если CLK равна 2 МГц, то наоборот - звуки будут выше примерно на 2 полутона (208 центов). Темп мелодии и относительные музыкальные погрешности не зависят от частоты CLK, чем и объясняется феномен высокой узнаваемости мелодии при широком варьировании тактовой частоты.
7. Из широко распространенных схем компьютеров 128К и приставок-128 более удачными следует признать решения с CLK=1,75 МГц ("АТМ-ТиЯВО-2" фирмы MicroART, самодельный Львовский вариант 128К и т.д.).
При этом высота каждой ноты будет ниже по сравнению с фирменным ZX-Spectrum-128 на 23 цента или на 1,3%.
Абсолютные погрешности звучания для 80 нот рабочей зоны гистограммы составят от 15 до 30 центов или от 0,9% до 1,7%. Относительные погрешности музыкальных интервалов определяются данными таблицы 5 и не будут отличаться от имеющихся в фирменном компьютере.
Литература.
1. Кунгуров А. Несколько устройств для "Спекки". - ZX-РЕВЮ 1994, №6, стр. 17-18.
2. Шепелев Г. Особенности подключения AY-3-8910 к Спектруму. - "Радиолюбитель", 1994, №3, стр.13.
3. Акустика. Справочник / А.П. Ефимов и др. Под ред. М.А. Сапожкова. - М.: Радио и связь, 1989.
4. Системные программы для ZX-Spectrum-128K. Справочник. - М.:'^ PRINT", 1993.
5. Моисеев А. Выбор коэффициентов деления частоты. - "Радио", 1990, №3, стр. 63-64.
6. Володин А. Основные технические требования к ЭМС. - "Радио", 1980, №2, стр. 42.
7. Советский энциклопедический словарь / Гл. ред. А.М. Прохоров. - М.: Сов. энциклопедия, 1987.