ГЛАВА 10

Простые алгоритмы удаления невидимых линий и

поверхностей

После того, как мы нарисовали куб и ещё несколько каркасных фигур, мы видим, что основным недостатком этих фигур является то, что они не воспроизводят реальных весомых тел. Нам бы хотелось рисовать реальные непрозрачные объекты, в которых передние грани делают невидимыми расположенные за ними грани и ребра. Для этой цели мы должны ввести алгоритмы удаления невидимых линий и поверхностей. Таких алгоритмов существует чрезвычайно много - некоторые из них элементарны и разработаны для специальных случаев, другие очень хитроумны и предназначены для работы со сложными объектами. Ограничения по времени, накладываемые использованием микрокомпьютера, не позволяет нам рассматривать очень сложные алгоритмы.

В случае SPECTRUMa накладывается дополнительное ограничение, запрещающее использовать в одном символьном блоке более двух цветов. Тем не менее, ограничив число типов и количество объектов в одном рисунке, можно добиться вполне удовлетворительных результатов. В главе 12 мы обсуждаем относительно сложный алгоритм, но здесь мы ограничимся двумя специальными типами сцен - мы используем свойства, явно заложенные в природе фигур, составляющих сцену, что облегчает задачу нахождения скрытых поверхностей и ребер. Ниже в этой главе мы приводим простой метод вычерчивания некоторых поверхностей в трёхмерном пространстве.

При определении алгоритма скрытых линий мы считаем, что информация о NOV вершинах объекта хранится в массивах X, Y, Z (в наблюдаемом положении). Однако, мы теперь будем использовать информацию о гранях, а не о ребрах. Информация о NOF-гранях хранится в массиве F (нам также необходим массив H, в котором хранится число вершин каждой многоугольной грани), а для сокращения объёма памяти ограничиваемся случаем, когда грань образуется не более, чем шестью ребрами.

Если требуются грани, содержащие большее число ребер, то такие грани следует разбивать на меньшие грани. Для того чтобы упростить алгоритм удаления невидимых линий, мы накладываем ограничение на порядок записи вершин в массиве F. Вершины следуют в порядке обхода грани так, что если на грань смотреть извне, то этот обход совершается против часовой стрелки. Естественно, что если смотреть изнутри объекта, то этот обход будет совершаться по часовой стрелке. Мы также полагаем, что каждая прямая находится на пересечении двух граней. Отдельные прямые, не связанные с гранями, добавляются в качестве вырожденных граней, ограниченных двумя ребрами.

Ориентация треугольника в трехмерном пространстве После определения объекта в терминах вершин и граней возникает вопрос: как проверить, что вершины действительно расположены в порядке обхода граней против часовой стрелки? Следует просто написать программу! Так как ориентация выпуклого многоугольника может быть определена по трём его последовательным точкам, то нам достаточно ограничиться случаем треугольника. В главе 7 мы уже познакомились со способом определения ориентации треугольника, расположенного на плоскости. Проблема будет решена, если нам удастся свести задачу к случаю двух измерений.

Для упрощения вычислений мы предполагаем, что объекты находятся в исходном положении и содержат начало координат. Мы предполагаем, что плоскости, в которых лежат грани, не проходят через начало координат. Совершим такое вращение пространства, чтобы одна из вершин рассматриваемого треугольника лежала на отрицательной половине Z (сравните с программой "LOOK3", приведенной на листинге 9.1). Так как мы предполагаем, что начало координат находится внутри объекта, то достаточно его спроецировать на плоскость X/Y (что просто означает отбрасывание значения Z-координаты) и рассматривать этот треугольник лежащим в этой плоскости (одна из его вершин будет в точке (0,0)). На листинге 10.1 приведено решение этой задачи. LISTING 10.1

100 REM ORIENTATION OF A 3-D TRIANGLE 110 DIM X(3): DIM Y(3): DIM Z(3) 120 DIM A(4,4):DIM B(4,4): DIM R(4,4)

130 LET ROT3=8600: LET ANGLE=8800: LET MULT3=9100: LET IDR3=9300 140 LET J$="TYPE IN COORDINATES ": LET K$="OF TRIANGLE " 150 FOR I=1 TO 3

160 LET I$="VERTEX("+STR$ I+")=(" 170 INPUT (J$+K$+I$);X(I);",";Y(I);",";Z(I);")" 180 PRINT AT 2+2*I,0;I$;X(I);",";Y(I);",";Z(I);")" 190 NEXT I

200 REM FIND MATRIX R THAT WILL PUT (X(1),Y(1),Z(1)) ON NEGATIVE Z-AXIS. 210 LET AX=X(1): LET AY=Y(1): GO SUB ANGLE

220 LET AXIS=3: LET THETA=-THETA: GO SUB ROT3: GO SUB MULT3 230 LET AX=Z(1): LET AY=SQR(X(1)*X(1)+Y(1)*Y(1)): GO SUB ANGLE 240 LET AXIS=2: LET THETA=PI-THETA: GO SUB ROT3: GO SUB MULT3

249 REM TRANSFORM TRIANGLE SO THAT ALL VERTICES TIE IN AN X/Y PLANE.

250 FOR I=1 TO 3

260 LET XX=X(I): LET YY=Y(I): LET ZZ=Z(I)

270 LET X(I)=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4)

280 LET Y(I)=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4)

290 NEXT I

299 REM CHECK IF THE NOW 2-D TRIANGLE IS CLOCKWIZE OR ANTI-CLOCKWIZE.

300 PRINT AT 11,0;"IF THE EYE AND THE ORIGIN ARE ON " 310 PRINT AT 13,0;"OPPOSITE SIDES OF THE FACET THEN" 320 PRINT AT 15,0;"THE TRIANGLE IS ";

330 LET DX1=X(2)-X(1): LET DY1=Y(2)-Y(1) 340 LET DX2=X(3)-X(2): LET DY2=Y(3)-Y(2) 350 IF DX1*DY2-DX2*DY1>0 THEN PRINT "ANTI-"; 360 PRINT "CLOCKWISE" 370 STOP Упражнение 10.1

Перепишите программы последней главы, предполагая, что информация задается с помощью вершин и ориентированных против часовой стрелки граней, а не с помощью линий. Проверяйте правильность исходных данных с помощью программы на листинге 10.1. Конечно же, информация о гранях включает явным образом информацию о рёбрах - каждое из них соединяет две последовательные вершины грани. Информация о каждом ребре содержится в массиве дважды - по одному разу в каждой из прилегающих к нему граней, а мы не хотим тратить время на то, чтобы чертить каждую линию дважды. Заметим, что, так как направление обхода всех граней против часовой стрелки, то если в одном случае ребро проходится от I до J, то при обходе другой грани оно пройдет от J до I, поэтому условимся чертить только те ребра, у которых индекс первой вершины меньше индекса второй вершины.

Алгоритм удаления скрытых поверхностей для случая тела, ограниченного замкнутой и выпуклой поверхностью Ограниченным выпуклым называется тело, которое вместе с любыми двумя внутренними точками содержит также и соединяющий их отрезок. Нетрудно видеть, что это не что иное, как обобщение определения, данного для двумерного случая. Это тело ограничено замкнутой поверхностью, и поэтому невозможно проникнуть внутрь тела, не пересекая его поверхности.

Ортогонально спроецируем все вершины тела на визуальную плоскость, заметив, что проекция выпуклого N-угольника есть выпуклый N-угольник (или вырождается в отрезок) на визуальной плоскости. Обходя вершины полученных N-угольников в той же последовательности, что и в оригинале, мы обнаружим, что наши двумерные многоугольники либо ориентированы против хода часовой стрелки, что означает, что мы смотрим на грань с внешней стороны тела, либо по ходу часовой стрелки, что означает, что мы смотрим на грань изнутри.

Так как объект ограничен замкнутой поверхностью, то мы не можем наблюдать грани с внутренней стороны -они являются невидимыми, а мы должны изобразить только видимые грани - получился довольно простой алгоритм, который может применяться как в конструирующих подпрограммах, так и в рисующей подпрограмме.

В качестве примера на рис. 37 приведено изображение куба, полученное с помощью усовершенствованной программы "CUBE", приведенной на листинге 10.2. В этом случае мы не храним информацию о гранях куба, а получаем информацию с помощью оператора READ из DATA и сразу же рисуем видимые грани. Мы используем все подпрограммы предыдущей главы, которые использовались для вычерчивания на рис. 33, кроме, конечно же, конструкционной подпрограммы, устанавливающей данные о вершинах и гранях, а затем вычерчивающей их (то есть мы заменяем подпрограмму на листинге 9.4 в программе, рисующей фигуру на рис. 33). Естественно, что мы

Упражнение 10.2

Измените, листинг 10.2 так, чтобы с помощью этой программы стало возможным вычерчивание изображения прямоугольного параллелепипеда длины LN, ширины BH и высоты HT, где LN, BH и HT - входные параметры подпрограммы. Затем нарисуйте тот же прямоугольник, но с удаленными невидимыми линиями. Нарисуйте тетраэдр, пирамиду, и т. д., удаляя при этом невидимые линии. Добавьте дополнительные параметры, с помощью которых можно искажать форму этого прямоугольного параллелепипеда, оставляя его при этом выпуклым.

LISTING 10.2

6500 REM CUBE/FACETS (NOT STORED) HIDDEN ELIMINATION

6501 REM IN - R(4,4)

6510 DATA 1,1,1,1,1,-1,1,-1,-1,1,-1,1,-1,1,1,-1,1,-1,-1,-1,-1,-1,-1,1

6520 DATA 1,2,3,4,5,8,7,6,1,5,6,2,2,6,7,3,7,8,4,1,4,8,5,1

6530 RESTORE CUBE

6539 REM PLACE VERTICES IN OBSERVED POSITION.

6540 FOR I=1 TO 8

6550 READ XX,YY,ZZ

6560 LET X(I)=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4)

6570 LET Y(I)=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4)

6580 NEXT I

6590 FOR I=1 TO 6

6599 REM Read facet information and draw it if oriented anti-c1ockwise.

6600 READ F1,F2,F3,F4

6610 LET DX1=X(F2)-X(F1): LET DY1=Y(F2)-Y(F1)

6620 LET DX2=X(F3)-X(F2): LET DY2=Y(F3)-Y(F2)

6630 IF DX1*DY2-DX2*DY1<0 THEN GO TO 6690

6640 LET XPT=X(F1) 6650 LET XPT=X(F2) 6660 LET XPT=X(F3) 6670 LET XPT=X(F4) 6680 LET XPT=X(F1) 6690 NEXT I 6700 RETURN

Тела вращения

Предложенный нами метод можно применять и для тел вращения, которые мы обсуждали в главе 9. На каждом из NUMH поворотов мы получаем NUMV граней. Если проследить за тем, чтобы при нумерации вершин этих граней соблюдалось правило обхода против часовой стрелки, то тогда применим метод предыдущего параграфа. На листинге 10.3 приведена такая программа; результат работы такой программы показан на рис. 38 - это та же фигура, что и на рис. 36, но с удалёнными невидимыми поверхностями. Опять-таки, в силу принятого нами модульного подхода все подпрограммы, необходимые для создания рис. 38, те же, что и в главе 9, за исключением процедуры "REVBOD". Теперь, однако, мы должны ограничиться только выпуклыми телами вращения.

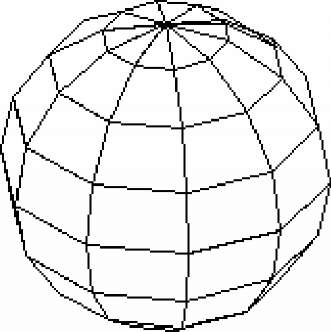
Рис. 38

Программа, по мере вращения вокруг вертикальной оси, хранит в памяти вершины двух последовательных вертикальных наборов отрезков, которые образуют "дольку", состоящую из граней. Вершины этих граней немедленно преобразуются матрицей R, соответствующей преобразованию, переводящему объект из исходного положения в наблюдаемое положение, и записывает их в массивы X и Y. Первое множество вершин вертикальных отрезков нумеруется от 1 до NUMV+(=N1), авторов множество от N1+1 до 2*N1. Первая грань ограничена четырьмя отрезками, двумя вертикальными, соединяющими вершину I с I+1 и I+N1 с I+N1+1 и двумя вертикальными отрезками, соединяющими точки I и I+N1, I+1 с I+N1+1.

Если грань вырождается в треугольную, то в описанную выше процедуру следует внести следующие изменения. Выбранный нами порядок вершин таков, что он соответствует обходу вершин против часовой стрелки, если смотреть с внешней стороны тела. Это позволяет применить простой алгоритм скрытых линий. Упражнение 10.3

Поэкспериментируйте с этой техникой. Для этой цели в качестве образующего набора годится любая выпуклая ломаная, оси которой лежат на оси Y. LISTING 10.3

6500 REM REVBOD/CONVEX BODY OF REVOLUTION (HIDDEN LINE ELIMINATION)

6501 REM IN - PHI,NUMH,NUMV,S(NUMV+1),R(4,4),T(NUMV+1) 6510 LET THETA=PHI: LET TD=PI*2/NUMH

6520 LET N1=NUMV+1: LET C=COS PHI: LET S=SIN PHI

6529 REM CREATE FIRST VERTICAL SET.

6530 FOR I=1 TO N1

6540 LET XX=S(I)*C: LET YY=T(I): LET ZZ=S(1)*S 6550 LET X(I)=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4) 6560 LET Y(I)=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4) 6570 NEXT I

6579 REM LOOP THROUGH SECOND VERTICAL SET.

6580 FOR J=1 TO NUMH

6590 LET THETA=THETA+TD: LET C=COS THETA: LET S=SIN THETA 6600 FOR I=1 TO N1

6610 LET XX=S(I)*C: LET YY=T(I): LET ZZ=S(I)*S 6620 LET X(I+N1)=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4) 6630 LET Y(I+N1)=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4) 6640 NEXT I

6649 REM TAKE ANTICLOCKWIZE TRIANGLE FROM EACH FACET BETWEEN THE TWO SETS. IF IT KEEPS ITS ORIENTATION ON PROJECTION THEN IT IS VISIBLE.

6650 FOR I=1 TO NUMV

6660 LET F1=I: LET F2=I+1: LET F3=F2+N1

6670 IF I=NUMV THEN LET F3=F3-1

6680 LET DX1=X(F2)-X(F1): LET DY1=Y(F2)-Y(F1)

6690 LET DX2=X(F3)-X(F2): LET DY2=Y(F3)-Y(F2)

6700 IF DX1*DY2-DX2*DY1<0 THEN GO TO 6770

6710 IF F3=F2+N1 THEN LET F4=F3-1

6720 LET XPT=X(F1): LET YPT=Y(F1): GO SUB MOVETO

6730 LET XPT=X(F2): LET YPT=Y(F2): GO SUB LINETO

6740 LET XPT=X(F3): LET YPT=Y(F3): GO SUB LINETO

6750 LET XPT=X(F4): LET YPT=Y(F4): GO SUB LINETO

6760 LET XPT=X(F1): LET YPT=Y(F1): GO SUB LINETO

6770 NEXT I

6779 REM COPY SECOND SET INTO FIRST AND REPEAT PROCESS.

6780 FOR I=1 TO N1

6790 LET X(I)=X(I+N1): LET Y(I)=Y(I+N1) 6800 NEXT I 6810 NEXT J 6820 RETURN

Вычерчивание поверхности специального вида, лежащей в трехмерном пространстве В этом разделе мы приводим алгоритм, позволяющий начертить фигуру, не являющуюся выпуклой, для этого используются некоторые особенности этой фигуры. Мы ограничиваемся случаем поверхностей в трёхмерном пространстве, задаваемых с помощью однозначной функции "F", зависящей от X и Z координат; "F" вычисляется в отдельной подпрограмме; в программе, приведенной на листинге 10.4, эта функция равна Y=4*SIN(XZ)/XZ, где XZ=SQRT(X**2+Z**2); а изображение, задаваемой этой функцией поверхности, приведено на рис. 39. Необходимые входные данные: HORIZ=32, VERT=22, (EX,EY,EZ)=(3,2,1), (DX,DY,DZ)=(0,0,0), NX=NZ=16, XMIN=ZMIN=-10, XMAX=ZMAX=10.

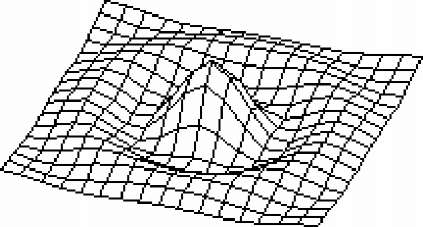
Рис. 39.

6690 LET YB=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4)

6700 GO SUB DRAWLIN

6710 LET XA=XB: LET YA=YB

6720 NEXT J

6729 REM MOVE X VALUES BACK IN NX STEPS.

6730 LET XS=XMAX 6740 FOR I=1 TO NX

6749 REM DRAW VISIBLE PARTS OF ONE FROM EACH OF THE FIXED Z-LINES. THE X VALUES VARY FROM (I-1)'ST X-LINE TO THE I'TH.

6750 LET ZS=ZMAX 6760 FOR J=1 TO NZ 6770 LET ZS=ZS-ZDIF

6780 LET XX=XS: LET ZZ=ZS: GO SUB F 6790 LET XA=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4) 6800 LET YA=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4) 6810 LET XX=XS-XDIF: GO SUB F

6820 LET XB=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4) 6830 LET YB=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4) 6840 GO SUB DRAWLIN 6850 NEXT J

6859 REM DRAW VISIBLE PARTS OF THE FIXED X-LINES.

6860 LET ZZ=ZMIN: GO SUB F

6870 LET XA=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4) 6880 LET YA=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4) 6890 FOR J=1 TO NZ 6900 LET ZZ=ZZ+ZDIF: GO SUB F

6910 LET XB=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4)

6920 LET YB=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4)

6930 GO SUB DRAWLIN

6940 LET XA=XB: LET YA=YB

6950 NEXT J

6960 LET XS=XS-XDIF

6970 NEXT I

6980 RETURN

7000 REM DRAWLIN/DRAW LINE BETWEEN POINTS

7001 REM IN - XA,YA,XB,YB,D(256)

7009 REM VISIBLE PARTS OF LINE BETWEEN (XA,YA) AND (XB,YB). IA AND IB ARE THE X-PIXEL POSITIONS OF THE TWO POINTS.

7010 LET IA=FN X(XA):LET IB=FN X(XB) 7020 LET Y=YA: LET YD=0

7030 IF IA<>IB THEN GO TO 7080 7040 PLOT IA,D(IA) 7050 LET IY=FN Y(YB)

7060 IF IY>D(IA) THEN DRAW 0,IY-D(IA): LET D(IA)=IY 7070 RETURN

7079 REM MOVE IN PIXEL COLUMNS FROM LEFT TO RIGHT.

7080 LET YD=(YB-YA)/(IB-IA) 7090 FOR K=IA TO IB

7100 LET IY=FN Y(Y)

7109 REM IF Y-PIXEL IS GREATER THAN D, THEN RESET D-VALUE.

7110 IF D(K)<IY THEN LET D(K)=IY 7120 LET Y=Y+YD

7130 NEXT K

7139 REM JOIN ALL THE POINTS (I,D(D) WHERE IA<=K<=IB.

7140 PLOT IA,D(IA) 7150 FOR K=IA+1 TO IB 7160 DRAW 1,D(K)-D(K-1) 7170 NEXT K

7180 RETURN

7200 REM F/FUNCTION TO BE DRAWN

7201 REM IN - XX,ZZ

7202 REM OUT - YY

7210 LET YY=4: LET XZ=SQR(XX*XX+ZZ*ZZ) 7220 IF XZ>0.000001 THEN LET YY=4*SIN(XZ)/XZ 7230 RETURN

Так как невозможно нанести все точки поверхности, то мы должны выделить подмножество этих точек,

которые мы выбираем в узлах сетки в плоскости X/Y; другими словами, если смотреть на поверхность сверху, т.е. спроецировать её на ось X/Z, отбросив значения Y-координат, то эти точки образуют прямоугольную сетку. Эта сетка состоит из прямоугольников размера NX на NZ, а X-координаты вершин прямоугольников расположены в интервале между XB и XT (XB<XT), и Z-координаты расположены в диапазоне от ZB до ZT (ZB<ZT). Таким образом, сетка состоит из (NX+1) X (NZ+1) вершин (X,Z), которые могут быть отождествлены с парой целых чисел (I,J) при помощи формулы:

X=XT+I*(XB-XT)/NX, где 0<=I<=NX Z=ZT+J*(ZB-ZT)/NZ, где 0<=J<=NZ

Точке на плоскости соответствует точка (X,Y,Z) на поверхности, где Y=F(X,Z). Каждая из (NX+1)*(NZ+1) точек сетки соединяется с каждым из своих четырёх непосредственных соседей по сетке (у этих точек одинаковые значения X или Z координат), за исключением точек, лежащих на границе сетки, которые соединяются с тремя точками, а в случае угловых точек - с двумя. Прямые, образующие сетку, можно считать состоящими из NX+1 отрезка, параллельного оси Y. Например, первый набор линий с фиксированным X состоит из NZ-прямых, соединяющих точки, соответствующие точкам от (I,J) до (I,J+1), где 0<=J<=NZ-1.

Поверхность может образовывать складки, так что не все точки поверхности будут видны с заданного положения глаза наблюдателя. Мы приводим простой алгоритм удаления невидимых линий, который просматривает точки поверхности от фронтальной части к тыльной.

Для упрощения алгоритма мы считаем, что глаз всегда находится в положительном квадранте (это означает, что EX>0, EY>0) и что взгляд направлен в начало координат (DX=DY=DZ-0). Если функция не симметрична, и мы хотим рассматривать её из другого квадранта, то для этого нам следует сменить знак Y, X или Z в выражении, определяющем функцию. После этого мы можем перевести поверхность в наблюдаемое положение. В этом положении мы сначала ортогонально проецируем на визуальную плоскость переднюю границу - две линии сетки с X=XZ и Z=ZT, соответствующие осям X и Y, после чего мы продвигаемся за NX шагов от переднего края к заднему. На I-ом шаге (1<=I<=NX) мы сначала рисуем видимые части отрезков, составляющих NZ Z-линий сетки. Другими словами, начиная с передней Z-линии сетки и продвигаясь назад, мы соединяем точки, лежащие на I-ой Х-линии с точками, лежащими на J-ой Х-линии сетки. После этого мы чертим видимые части набора отрезков, составляющих I-ую линию. Этот алгоритм реализован в программе "SURFACE".

До сих пор мы не объясняли, как чертить видимые части линий; эту работу выполняет подпрограмма "DRAWLIN". Мы определяем массив D, содержащий 256 элементов, каждый из которых соответствует столбцу элементов изображения на экране; затем чертим нулевую прямую с фиксированным X и нулевую прямую с фиксированным Z линиями. Для каждой точки этих линий заносим в массив D координаты элемента изображения, соответствующего этим точкам. Для каждого элемента изображения, лежащего на данном отрезке, мы вычисляем значение строки и столбца и наносим этот элемент, если только значение столбца больше, чем значение, записанное в массиве. Каждый раз, когда к рисунку добавляется новый элемент изображения, изменяется значение соответствующего элемента массива D.

В данном алгоритме существенно, в каком порядке мы рассматриваем прямые. Если мы начинаем с положительного квадранта или если поверхность выходит за границы экрана, то наш алгоритм непригоден.

Упражнение 10.4

Измените функцию "F", используемую в программе. Например, используйте F=4*SIN(T), где T=SQRT(X**2+Y**2).

Упражнение 10.5

Наша программа не позволяет изобразить на экране те куски поверхности, которые лежат ниже нулевых X и Z линий. Измените программу на листинге 10.4 с тем, чтобы исправить этот недостаток. Для этого введите массив E, который первоначально содержит информацию о ближайших краях, а когда значение элемента изображения оказывается меньше того, что содержится в массиве E, то этот элемент наносится на экран, и производится соответствующеё изменение в массиве E.

Список программ

1. "LIB3" и листинг 10.1. Необходимые данные: координаты X(I), Y(I), Z(I) вершин треугольников, где 1<I<3. Попробуйте ввести значения 1, 0, 1, 1, 1, 0, 0, 1, 0, а также эти вершины в другом порядке -1, 1, 0, 1, 0, 1 ,0, 1, 1.

2. "LIB1", "LIB3" и листинги 9.5 ("SCENE3") и 10.2 ("CUBE"). Необходимая информация: HORIZ, VERT, (EX,EY,EZ), (DX,DY,DZ). Попробуйте ввести значения 9, 6, (1,2,3), (0,0,-1).

3. "LIB1", "LIB3" и листинг 9.10 ("SCENE3") и 10.3 ("REVBOD"). Входные данные: HORIZ, VERT, NUMH, NUMV (<=15), PHI, (EX,EY,EZ), (DX,DY,DZ). Попробуйте ввести значения 3.2, 2.2, 10, 6, 1, (1,2,3), (0,0,-1).

4. "LIB1", "LIB3" и листинг 10.4 ("SCENES", "SURFACE", "DRAWLIN" и "F"). Входные данные: HORIZ, VERT, (EX,EY,EZ), (DX,DY,DZ), NX, XMIN, XMAX, NZ, ZMIN, ZMAX. Попробуйте ввести значения 30, 20, (1,2,3), (0,0,0), 16, -8, 8, 18, -8, 16.

1. Предисловие - данная книга является введением в предмет компьютерной графики, может рассматриваться как дешевый пакет программ.
2. Введение - Эту книгу можно можно рассматривать как книгу рецептов графических программ, позволяющих рисовать сложные картинки с помощью SPECTRUMa.
3. Графические команды ZX SPECTRUM - Команды PAPER и INK; Дисплейный файл; Команда BORDER; Символьные блоки; Команды PLOT и DRAW; Команды PRINT и LIST; Команды INVERSE и OVER; Команды FLASH и BRIGHT; Атрибуты; Простейшее движущееся изображение; Команды CIRCLE и DRAW; Цвета в символьном блоке; Простая игра.
4. От реальных координат к пикселям - Примитивы, обеспечивающие карту пространства на графическом экране; Список программ;
5. Геометрия декартовой плоскости - Кадрирование; Задание кривых с помощью функциональной зависимости; Список программ.
6. Матричное представление преобразований двумерного пространства - Композиция преобразований; Перенос; Растяжение; Вращение относительно начала координат; Обратное преобразование; Размещение объекта; Рассматривание объекта; Вычерчивание объекта; Сложные изображения - метод построения изображения "по кирпичикам"; Эффективное использование матриц; Хранение информации об изображении; Список программ.
7. Символьная графика ZX SPECTRUM - Стандартный набор символов; Графический режим работы; Блочная графика; Графика, определяемая пользователем; Альтернативные множества символов; Список программ.
8. Диаграммы и графики - Курсоры; Атрибуты; Точки и линии; Запись и загрузка; Надписи; Данные для графиков; Специальные символы; Определенные пользователем символы для использования в гистограммах; Гистограммы; Круговые диаграммы; Штриховка секторов; Графики; Список программ.
9. Трёхмерная декартова геометрия - Определение прямой; Угол между двумя направляющими векторами; Определение плоскости70 Точка пересечения прямой и плоскости; Расстояние от точки до прямой; Точка пересечения двух прямых; Плоскость, проходящая через три неколлинеарные точки; Точка пересечения трёх плоскостей; Линия пересечения двух плоскостей; Функциональное представление поверхности; Лежит ли точка по ту же сторону от плоскости, что и начало координат?; Каково направление обхода двумерного многоугольника, заданного последовательностью своих вершин?
10. Матричное представление преобразования трехмерного пространства - Параллельный перенос; Растяжение; Вращение относительно координатной оси; Вращение на угол ТЕТА относительно оси X; Обратное преобразование; Поворот на угол NU относительно произвольной оси.
11. Ортогональные проекции - Исходное положение; Фактическое положение; Наблюдаемое положение; Ортогональная проекция; Вычисление матрицы Q, переводящей объект из фактического положения в наблюдаемое; Как задавать объект; Конструирующие подпрограммы и метод построения блоков; Тела вращения.
12. Простые алгоритмы удаления невидимых линий и поверхностей - Ориентация треугольника в трехмерном пространстве; Алгоритм удаления скрытых поверхностей для случая тела, ограниченного замкнутой и выпуклой поверхностью; Тела вращения; Вычерчивание поверхности специального вида, лежащей в трехмерном пространстве.
13. Перспективная проекция - Что такое перспективное видение? Построение перспективной проекции точки; Свойства перспективной проекции; Выбор визуальной плоскости; Кадрирование изображения; Список программ.
14. Общий алгоритм удаления невидимых линий - алгоритм для перспективного отображения трехмерного обьекта, хранящегося в памяти.
15. Белее сложные элементы программирования - Управление выполнением программ; Структура дисплейного файла; Быстрое преобразование содержимого экрана; Мультипликация; Свертка; Структура программ на бейсике (перенумерация и уничтожение); Структура программы на бейсике (эффективные программы); Синхронное изображение.
16. Действующий пример видеоигры - Описание игры; Передний план; Фон; Каскадная мультипликация; Другие методы мультипликации.
17. Проекты - ПРИЛОЖЕНИЕ А.