ГЛАВА 8
Матричное представление преобразования трехмерного пространства
Представление преобразования переноса, вращения, растяжения (отражения) трёхмерного пространства с помощью матриц четыре на четыре
• Обратное преобразование
• Композиция преобразований
• Вращение вокруг произвольной оси
ВНИМАНИЕ! Тем нашим читателям, которые слабо представляют себе матрицы и операции над ними, советуем сначала внимательно прочитать главу 4 данной книги, где популярно описываются основы матричных преобразований и подробно рассматриваются вопросы матричного представления двумерного пространства.
Здесь же мы предлагаем читателю дальнейшее развитие теории матричного представления пространства уже для трёх измерений. Ниже мы приводим готовую программу умножения двух матриц для трёхмерного случая (см.
|
листинг 8.1). |
|
|
LISTING 8.1 |
|
9100 |
REM MULT3 |
|
9101 |
REM IN - A(4,4),R(4,4) |
|
9102 |
REM OUT - R(4,4) |
|
9110 |
FOR I=1 TO 4 |
|
9120 |
FOR J=1 TO 4 |
|
9130 |
LET AR=0 |
|
9140 |
FOR K=1 TO 4 |
|
9150 |
LET AR=AR+A(I,K)*R(K,J) |
|
9160 |
NEXT К |
|
9170 |
LET B(I,J)=AR |
|
9180 |
NEXT J |
|
9190 |
NEXT I |
|
9200 |
FOR I=1 TO 4 |
|
9210 |
FOR J=1 TO 4 |
|
9220 |
LET R(I,J)=B(I,J) |
|
9230 |
NEXT J |
|
9240 |
NEXT I |
|
9250 |
RETURN |
|
9300 |
REM IDR3 |
|
9302 |
REM OUT - R(4,4) |
|
9310 |
FOR I=1 TO 4 |
|
9320 |
FOR J=1 TO 4 |
|
9330 |
LET R(I,J)=0 |
|
9340 |
NEXT J |
|
9350 |
LET R(I,I)=1 |
|
9360 |
NEXT I |
|
9370 |
RETURN |
Рассмотрим уравнение: 1=A*X+A*Y+A*Z+A
Его справедливость для всех X,Y означает A(4,1)=A(4,2)=A(4,3)=0 и A(4,4)=1. Эти уравнения могут быть записаны в матричной форме, где вектор-столбец, соответствующий точке "после", есть произведение матрицы на столбец "до".
|
(X1 |
( A(1,1) |
A(1,2) |
A(1,3) |
A(1,4) > |
|
f x 1 |
|
Y' |
A(2,1) |
A(2,2) |
A(2,3) |
A(2,4) |
v |
Y |
|
Z' |
" A(3,1) |
A(3,2) |
A(3,3) |
A(3,4) |
A |
Z |
|
( 1 , |
I A(4,1) |
A(4,2) |
A(4,3) |
A(4,4) ; |
|
( 1 S |
Так что если мы запишем преобразование в виде матрицы и сохраним её, то мы можем преобразовать любые точки умножением соответствующих им вектор-столбцов на матрицы. Как и ранее, имея матричную запись преобразований, легко составить преобразование, соответствующее композиции этих преобразований. Если матрицы преобразований есть (в порядке совершения преобразований) A,B,C...L,M,N, то матрица результирующего преобразования есть N*M*L*C*B*A. Запомните последовательность. Она связана с тем, что мы оперируем с вектор-столбцами, а не вектор-строками.
Параллельный перенос
Пусть совершается параллельный перенос на вектор (TX,TY,TZ). Этому преобразованию соответствуют уравнения:
X' = 1*Х+0 *Y+0 *Z+TX Y' = 0*X-1*Y+0*Z+TY
Z' = 0 *X-0 * Y+1 *Z+TZ которым в свою очередь соответствует матрица
|
Г1 |
0 |
0 |
TX N |
|
0 |
1 |
0 |
TY |
|
0 |
0 |
1 |
TZ |
|
v 0 |
0 |
0 |
1 , |
Подпрограмма "TRAN3" генерирует такую матрицу по заданным параметрам ТХ, TY, TZ (см. листинг 8.2). LJSTING 8.2
9000 REM TRAN3
9001 REM IN - TX,TY,TZ
9002 REM OUT - A(4,4) 9010 FOR I=1 TO 4 9020 FOR J=1 TO 4 9030 LET A(I,J)=0 9040 NEXT J
9050 LET A(I,I)=1 9060 NEXT I
9070 LET A(1,4)=TX: LET A(2,4)=TY: LET A(3,4)=TZ 9080 RETURN
Растяжение
Если масштабные множители растяжения по оси X, Y и Z есть X, Y и Z соответственно, то уравнения преобразования:
X'=SX*X+0*Y+0*Z+0 Y'=0 *X+SY*Y+0 *Z+0 Z'=0*X+0*Y+SZ*Z+0
и соответствующая ему матрица:
|
' SX |
0 |
0 |
01 |
|
0 |
SY |
0 |
0 |
|
0 |
0 |
SZ |
0 |
|
v 0 |
0 |
0 |
1, |
Обычно масштабные множители положительны, однако, если какой-либо из этих множителей отрицателен, то преобразование является композицией отражения и растяжения. Например, значениям SX=-1, SY=1, SZ=1 соответствует отражение относительно плоскости X/Y. Подпрограмма "SCALES" генерирует матрицу преобразования A по заданным SX, SY, SZ (см. листинг 8.3). LISTING 8.3
8900 REM SCALE3
8901 REM IN - SX,SY,SZ
8902 REM OUT - A(4,4) 8910 FOR I=1 TO 4 8920 FOR J=1 TO 4 8930 LET A(I,J)=0 8940 NEXT J
8950 NEXT I
8960 LET A(1,1)=SX: LET A(2,2)=SY: LET A(3,3)=SZ 8970 LET A(4,4)=1 8980 RETURN
Вращение относительно координатной оси Прежде чем изучать вращение относительно оси P-MU*Q на заданный угол рассмотрим более простой случай вращения относительно координатной оси.
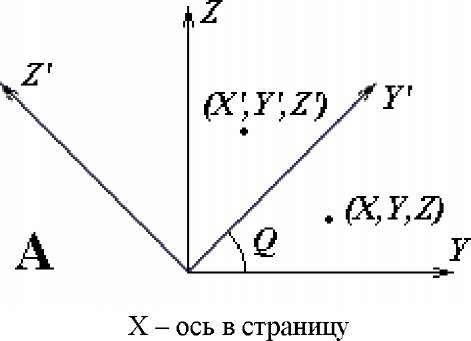

Z - ось в страницу Рис. 32.
(A) Х-ось направлена в плоскость страницы;
(Б) Y-ось направлена в плоскость страницы;
(B) Z-ось направлена в плоскость страницы.
(A) Вращение на угол ТЕТА относительно оси X
На рис. 32А ось вращения направлена перпендикулярно плоскости страницы (положительной полуосью от читателя); на рисунке показана точка (X',Y',Z'), в которую переходит точка (X,Y,Z) в результате вращения. Мы видим, что вращение сводится к вращению в двумерной плоскости, что означает, что Х-координаты точки при таком преобразовании не меняются. Используя методы главы 4, мы получим уравнение:
= X
COS ТЕТА * Y - SIN ТЕТА * Z SIN ТЕТА * Y + COS ТЕТА * Z,
которому соответствует матрица:
о ^
00 о COS TETA - SIN TETA 0 0 SIN TETA COS TETA 0 00
0
(Б) Вращение на угол ТЕТА относительно оси Y
На рисунке 32Б показано вращение плоскости на угол Q относительно оси Y, положительная полуось которой направлена от читателя и перпендикулярна плоскости страницы. Это вращение задается уравнением:
X' = SIN ТЕТА *Z + COS ТЕТА *Х Y' = Y
Z' = COS ТЕТА * Z - SIN ТЕТА * X, и соответствующая этому преобразованию матрица:
Г COS TETA 0 SIN TETA 0^
0
- SIN TETA 0 COS TETA 0
0
v v
(B) Вращение на угол ТЕТА относительно оси Z
Согласно рисунку имеем:
X' = COS ТЕТА * X - SIN ТЕТА * Y
Y' = SIN ТЕТА * X + COS ТЕТА * Y
Z' = Z
и матрица:
|
fCOS TETA |
- SIN TETA |
0 |
01 |
|
SIN TETA |
COS TETA |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
v 0 |
0 |
0 |
1J |
Подпрограмма "ROT3" генерирует необходимую матрицу по значениям двух параметров - углу ТНЕТА и номеру оси AXIS (1 - соответствует оси X, 2 - оси Y, 3 - оси Z). Программа приведена на листинге 8.4. LISTING 8.4
8600 REM ROT3
8601 REM IN - THETA,AXIS
8602 REM OUT - A(4,4) 8610 FOR I=1 TO 4 8620 FOR J=1 TO 4 8630 LET A(I,J)=0
8640 NEXT J 8650 NEXT I
8660 LET A(4,4)=1: LET A(AXIS,AXIS)=1 8670 LET AX1=AXIS+1: IF AX1=4 THEN LET AX1=1 8680 LET AX2=AX1+1: IF AX2=4 THEN LET AX2=1 8690 LET CT=COS THETA: LET ST=SIN THETA 8700 LET A(AX1,AX1)=CT: LET A(AX2,AX2)=CT 8710 LET A(AX1,AX2)=-ST: LET A(AX2,AX1)=ST 8720 RETURN
Обратное преобразование Прежде чем изучать общий вид вращения трёхмерного пространства, мы ознакомимся с понятием обратного преобразования. Обратное преобразование возвращает точки, переведенные заданным преобразованием, в исходные. Если преобразование задается матрицей A, то обратное преобразование задается матрицей A**(-1), обратной к A. Нам не потребуется явное вычисление обратной матрицы такими методами, как, например, присоединенный метод (листинг 7.5). Мы можем использовать программы на листингах 8.2, 8.3, 8.4 с параметрами, полученными из значений параметров исходного преобразования.
1) Параллельный перенос на вектор (TX,TY,TZ), обратное преобразование - параллельный перенос на вектор (-TX,-TY,-TZ);
2) Растяжение на SX, SY, SZ; обратное преобразование - растяжение на 1/SX, 1/SY, 1/SZ;
3) Поворот на угол ТНЕТА относительно оси; обратное преобразование - поворот на угол ТНЕТА относительно той же оси;
4) Если преобразование является композицией нескольких преобразований параллельного переноса, вращения, растяжения матриц A*B*C*...*L*M*N, тогда обратное преобразование есть N-1 *М-1 *L-1 *.*С-1 *В-1 * А-1.
Поворот на угол NU относительно произвольной оси P+MU*Q Положим P=(PX,PY,PZ), Q=(QX,QY,QZ). Разобьём задачу на следующие этапы:
А) Преобразуем, точки пространства так, чтобы ось вращения проходила через начало координат. Это достигается параллельным переносом на вектор (-PX,-PY,-PZ); матрица этого преобразования E генерируется вызовом процедуры "TRAN3" со значением параметров (-PX,-PY,-PZ). Обратная к этой матрице, матрица E, генерируется вызовом процедуры "TRAN3" со значением параметров (PX,PY,PY).
|
Г1 |
0 |
0 |
- PX 1 |
|
г 1 |
0 |
0 |
PX Л |
|
0 |
1 |
0 |
- PY |
|
0 |
1 |
0 |
PY |
|
|
|
|
|
E- = |
|
|
|
|
|
0 |
0 |
1 |
- PZ |
|
0 |
0 |
1 |
PZ |
|
v 0 |
0 |
0 |
1 J |
|
v 0 |
0 |
0 |
1J |
Б) Теперь повернем точки пространства на угол ALPHA, где ALPHA=ARCTG (QY/QX); этому преобразованию соответствует матрица G, которая генерируется вызовом подпрограммы "ROT3" со значением параметров TETA=-ALPHA, AXIS=3. После выполнения такого преобразования ось вращения лежит в плоскости X/Z и проходит через точку (Y,0,QZ).
(
|
QX |
QY |
0 |
0 1 |
|
- QY |
QX |
0 |
0 |
|
0 |
0 |
NU |
0 |
|
0 |
0 |
0 |
NUJ |
где NU>0: NU**2=QX**2+QY**2
В) Теперь повернем точки плоскости относительно оси Y на угол -BETA, где BETA=ARCTG(NU/QZ); соответствующую матрицу обозначим H. Эта матрица генерируется вызовом "ROT3" со значением параметров AXIS=2 и THETA=BETA.
H =■
|
|
f QZ
ff 0 |
0 |
- NU |
01 |
|
f QZ
ff 0 |
0 |
NU |
01 |
|
1 |
|
W |
0 |
0 |
, 1 |
|
W |
0 |
0 |
|
|
|
|
|
|
H- = — |
|
|
|
|
|
W |
NU
ffv 0 |
0 |
QZ |
0 |
W |
- NU ffv 0 |
0 |
QZ |
0 |
|
|
|
0 |
0 |
1J |
|
|
0 |
0 |
1J |
где W задается соотношением:
W**2=NU**2+QZ**2=QX**2+QY**2+QZ**2. Точка (NU,0,QZ) переводится в точку (0,0,W) и, следовательно, ось вращения теперь совпадает с осью Z.
Г) Теперь мы можем повернуть точки пространства на угол GAMMA относительно оси вращения, используя матрицу W, сгенерированную вызовом "ROT3" (со значением
|
(COS (GAMMA) |
- SIN (GAMMA) |
0 |
01 |
|
SIN (GAMMA) |
COS(GAMMA) |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
v 0 |
0 |
0 |
1J |
AXIS=3 и THETA=GAMMA).
Д) Установим ось вращения в исходное положение с помощью преобразований с матрицами H-1, G-1 и, наконец, F-1.
В окончательном виде матрица P вращения точек пространства относительно оси P+M*Q на угол GAMMA задается в виде
P=F-1*G-1*H-1*W*H*F.
В некоторых случаях эти матрицы равны тождественной и не влияют на вид преобразования. Например, если ось вращения проходит через начало координат, то матрицы F и F-1 равны тождественной, и ими можно пренебречь.
Программа "GENROT" (листинг 8.5) вычисляет матрицу вращения P по заданным входным параметрам GAMMA, (PX,PY,PZ) и (QX.QY.QZ). LISTING 8.5
5800 REM GENROT
5801 REM IN - PX,PY,PZ, QX,QY,QZ, GAMMA,R(4,4)
5802 REM OUT - R(4,4)
5809 REM PLACE ORIGIN ON AXIS OF ROTATION.
5810 LET TX=PX: LET TY=PY: LET TZ=-PZ: GO SUB TRAN3: GO SUB MULT3
5819 REM ROTATE AXIS OF ROTATION INTO X/Z PLANE.
5820 LET AX=QX: LET AY=QY: GO SUB ANGLE
5830 LET ALPHA=THETA: LET THETA=-THETA: LET AXIS=3: GO SUB ROT3: GO SUB MULT3
5839 REM ROTATE AXIS OF ROTATION INTO Z-AXIS.
5840 LET AX=QZ: LET AY=SQR(QX*QX+QY*QY): GO SUB ANGLE
5850 LET BETA=THETA: LET THETA=-THETA: LET AXIS=2: GO SUB ROT3: GO SUB MULT3
5859 REM ROTATE BY GAMMA ABOUT AXIS OF ROTATION.
5860 LET THETA=GAMMA: LET AXIS=3: GO SUB ROTS: GO SUB MULT3
5869 REM REPLACE AXIS BACK TO ORIGINAL POSITION.
5870 LET THETA=BETA: LET AXIS=2: GO SUB ROT3: GO SUB MULT3 5880 LET THETA=ALPHA: LET AXIS=3: GO SUB ROT3: GO SUB MULT3 5890 LET TX=PX: LET TY=PY: LET TZ=PZ: GO SUB TRAN3: GO SUB MULT3 5900 RETURN
Пример 8.А
Куда перейдут точки (0,0,0), (1,0,0), (0,1,0) и (0,0,1), (1,1,1) при повороте на PI/4 относительно оси (1,0,1)
(3,4,5).
Используя изложенную выше теорию, получим:
(1 0 0 - 11
|
|
-4 |
0 |
01 |
|
|
3 |
0 |
0 |
|
|
0 |
5 |
0 |
|
|
0 |
0 |
5J |
|
1 |
0 |
1 |
01 |
|
0 |
2 |
0 |
0 |
|
-1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
2J |
0 1 0 0 0 0 1 -1
|
v0 |
0 |
0 |
1J |
|
(3 |
4 |
0 |
01 |
|
- 4 |
3 |
0 |
0 |
|
0 |
0 |
5 |
0 |
|
v0 |
0 |
0 |
5, |
|
(1 |
0 |
-1 |
01 |
|
0 |
2 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
v0 |
0 |
0 |
2J |
|
(1 |
-1 |
0 |
01 |
|
1 |
1 |
0 |
0 |
|
0 |
0 |
2 |
0 |
|
v0 |
0 |
0 |
2J |
где P=F"1*G"1*H"1*W*H*G*F - матрица, соответствующая искомому преобразованию. Умножая вектор-столбцы,
соответствующие (0,0,0), (1,0,0), (0,0,1), (1,1,1), на матрицу P, переводя получившиеся столбцы в строчную форму и вынося фактор 1/50*SQRT(2), получим новые координаты (-26+6SQRT2, 32-42SQRT2, -10+30SQRT2), (15+15sQrT2, 20-5SQRT2, -25+25SQRT2), (-38-7SQRT2, 66-26SQRT2, -3+65SQRT2), (-41+41SQRT2, 12-37SQRT2, 15+55SQRT2), (12+37SQRT2, 34+16SQRT2, -20+85SQRT2) соответственно.
Естественно, что вращение не меняет взаимного расположения точек; в частности, углы между прямыми не изменяются (что неверно для растяжения, которое в общем случае меняет взаимное расположение прямых). В исходном положении направления от (0,0,0) к (1,0,0), (0,1,0), (0,0,1) взаимно перпендикулярно (что означает равенство нулю скалярного произведения). Скалярное произведение преобразованных направлений должно быть равным нулю; действительно, три направляющих вектора (с точностью до множителя 1/50SQRT2) есть (41+9SQRT2, -12+37SQRT2, -15-5SQRT2), (-12-13SQRT2, 34+16SQRT2, -20+35SQRT2) и (-15+35SQRT2, -20+5SQRT2, 25+25SQRT2) и скалярное произведение любой пары равно нулю.
Аналогично, скалярное произведение направляющего вектора (1,1,1) с любым из направлений, перечисленных выше, равно 1. То же верно и для направлений после преобразования: четвёртое направление -(14+31SQRT2, 2+58SQRT2, -10+55SQRT2), а скалярное произведение с любым из трех направлений есть 5000, что после деления на (59SQRT2) даёт 1.
Программа, которая считывает параметры, задающие ось вращения (PX,PY,PZ)+M(QX,QY,QZ) и угол вращения GAMMA и поворачивает точку (XX,YY,ZZ), приведена на листинге 8.6. LISTING 8.6
100 REM ROTATION OF A POINT ABOUT A GIVEN AXIS 110 DIM A(4,4): DIM B(4,4): DIM R(4,4) 120 DIM P(3): DIM A$(8)
130 INPUT "BASE VECTOR OF AXIS ","(";PX;",";PY;",";PZ;")"
140 PRINT AT 1,0;"BASE VECTOR OF AXIS","(";PX;",";PY;",";PZ;")"
150 INPUT "DIRECTION VECTOR OF AXIS ","(";QX;",";QY;",";QZ;")"
160 PRINT AT 4,0;"DIRECTION VECTOR OF AXIS","(";QX;",";QY;",";QZ;")"
170 INPUT "ANGLE OF ROTATION ",-GAMMA
180 PRINT AT 7,0;"ANGLE OF ROTATION "-GAMMA
190 LET MULT3=9100: LET IDR3=9300: LET ROT3=8600: LET TRAN3=9000: LET ANGLE=8800: LET GENROT=5800
199 REM CALCULATE R(4,4) FOR ROTATING POINT BY ANGLE GAMMA ABOUT AN AXIS WITH BASE VECTOR (PX,PY,PZ) AND DIRECTION VECTOR (QX,QY,QZ)
200 GO SUB IDR3: GO SUB GENROT 210 PRINT AT 14,0;"BECOMES"
219 REM INPUT AND TRANSFORM POINT (XX,YY,ZZ).
220 INPUT "POINT VECTOR ","(";XX;",";YY;",";ZZ;")" 230 PRINT AT 12,0;"POINT (";XX;",";YY;",";ZZ;")",, 240 LET P(1)=XX*R(1,1)+YY*R(1,2)+ZZ*R(1,3)+R(1,4) 250 LET P(2)=XX*R(2,1)+YY*R(2,2)+ZZ*R(2,3)+R(2,4) 260 LET P(3)=XX*R(3,1)+YY*R(3,2)+ZZ*R(3,3)+R(3,4)
269 REM TIDY UP OUTPUT.
270 PRINT AT 16,0;" (";
280 FOR I=1 TO 3: LET A$=STR$ P(I): FOR J=1 TO 8
290 IF A$(J)<>" "THEN PRINT A$(J);
300 NEXT J: IF I<>3 THEN PRINT",";
310 NEXT I: PRINT ")",,
320 GO TO 220
Упражнение 8.1
Поэкспериментируйте с этими идеями. Вы всегда можете проверить правильность своего решения, выбрав значения, для которых легко найти решение. Для дальнейшего важно, чтобы вы освоились в совершенстве с матричным исчислением, а это достигается только опытом. Сначала вас будут преследовать арифметические ошибки, но через некоторое время вы привыкнете думать о преобразованиях в терминах матриц, что значительно облегчает изучение способов изображения трехмерных объектов. Упражнение 8.2
Заметим, что, так же как и в двумерном случае, нижняя строка любой матрицы, соответствующей преобразованию трёхмерного пространства, всегда есть (0,0,0,1) и не используется при вычислениях. Эта строка позволяет нам представлять преобразования в виде квадратных матриц, а для квадратных матриц, в свою очередь, определить операцию умножения. Мы можем изменить это определение с тем, чтобы перемножать матрицы и умножать вектор-столбцы на матрицы, используя только верхние три строки матриц 4*4 (в главе 4 мы использовали в программах, приведенных на листингах 4.2А, 4.3А, 4.4А, 4.5А, две верхние строки матриц 3*3). Измените листинги 8.1, 8.2, 8.3 и 8.4 с учётом нового определения. Упражнение 8.3
Подпрограмма "ROT3" вычисляет величину THETA, вызывая подпрограмму "ANGLE", входными параметрами которой являются величины AX и AY. Подпрограмма "ROT3" вычисляет косинус и синус угла THETA, но мы знаем, что последние равны AX/SQRT(AX**2+AY**2) и AY/SQRT(AX**2+AY**2) соответственно.
Напишите другую подпрограмму, осуществляющую вращение "ROTXY", которая вычисляла бы матрицу вращения непосредственно AX и AY, не обращаясь к подпрограмме "ANGLE".
Обратите также внимание на то, что в начале своей работы подпрограммы "ROT", "TRAM", "SCALE", и "IDR" очищают массив. SPECTRUM производит эту операцию быстрее, если используется команда DIM. Кроме того, зачастую непосредственные присвоения элементам массива значений выполняется быстрее, чем присвоения в циклах FOR...NEXT.
Упражнение 8.4
Ещё раз отметим, что некоторые авторы предпочитают использовать вектор-строки вместо вектор-столбцов, что приводит к иному порядку сомножителей при композиции преобразований. Наши обозначения имеют то преимущество, что элементы матрицы есть в точности коэффициенты уравнения, определяющего преобразования.
Полезно также помнить и о другом способе представления преобразований; используйте его и перепишите все подпрограммы этой главы, а также оставшейся части книги. Помните, что не важно, какой метод использовать, важно только остановить свой выбор на одном из них раз и навсегда. Мы используем вектор-столбцы потому, что считаем его наиболее подходящим на ранней стадии обучения.
Список программ
1. Все листинги в этой главе, 8.1 ("MULT3" и "IDR3"), 8.2 ("TRAN3"), 8.3 ("SCALES"), 8.4 ("ROT3"), 8.5 ("GENROT"), 8.6 (MAIN PROGRAM) и листинг 3.4 ("ANGLE"). Входные данные: базисный вектор (PX,PY,PZ) и направляющий вектор (QX,QY,QZ) оси вращения, угол, на который производится вращение - GAMMA, а также любой вектор с тремя компонентами - (XX.YY.ZZ). Введите, например, (0,0,0), (1,1,1) и PIMmm^ (1,0,1), (1,1,1), (1,2,3).