ZX Spectrum графика - Матричное представление преобразований двумерного пространства - Композиция преобразований; Перенос; Растяжение; Вращение относительно начала координат; Обратное преобразование; Размещение объекта; Рассматривание объекта; Вычерчивание объекта; Сложные изображения - метод построения изображения "по кирпичикам"; Эффективное использование матриц; Хранение информации об изображении; Список программ.

1994 г.

Матричное представление преобразований двумерного пространства - Композиция преобразований; Перенос; Растяжение; Вращение относительно начала координат; Обратное преобразование; Размещение объекта; Рассматривание объекта; Вычерчивание объекта; Сложные изображения - метод построения изображения "по кирпичикам"; Эффективное использование матриц; Хранение информации об изображении; Список программ.

ГЛАВА 4

Матричное представление преобразований двумерного

пространства

В главе 2 у нас возникла необходимость перемещать объекты по экрану. Представляется более удобным сначала определять объект в простейших терминах (таких, как вершины в терминах пикселей или значений координат, вместе с информацией о линиях и областях, связанных с этими вершинами), а затем помещать эти объекты в нужное место на экране, оставляя при этом систему координат экрана неподвижной. Мы ограничимся случаем линейных перемещений (преобразований).

Иногда бывает необходимо переместить большое количество вершин, и в этом случае чрезвычайно полезным оказывается понятие матрицы. Перед тем, как ввести матричное представление преобразований, определим сначала, что мы подразумеваем под словом матрица, и введем понятие вектора-столбца.

На самом деле мы ограничимся случаем матрицы 3x3 (произносится: три на три) для изучения двумерной геометрии, а позже, при изучении геометрии, мы будем использовать матрицы 4Х4. Такая 3Х3 матрица - это не что иное, как таблица чисел, состоящая из трех строк и трех столбцов, а вектор-столбец - это столбец чисел, состоящий из трех чисел.

A (l,l) A(l,2) A(l,3) D1

А (2,1) А(2,2) А(2,3) и D2

A(3,l) A(3,2) A(3,3) D3

Элемент матрицы имеет вид A(I,J), где I - это номер строки, в которой расположен этот элемент, J - номер столбца (например, А(2,3) расположен во второй строке и третьем столбце). Все элементы являются числами, и важно помнить, что информация, записанная в столбце матрицы, состоит из значений чисел, составляющих этот столбец и расположения столбца в матрице. Символы в программе, написанной, на бейсике, расположены в строчку, и полому матрицы и вектора записываются также в строчку с индексами, заключенными и скобки и следующими за идентификатором матрицы.

Матрицы можно складывать. Матрица A+B, сумма матриц A и B, элемент которой C(I,J) по определению

равен:

C(I,J)=A(I,J)+B(I,J) 1<=I, J<=3

Умноженная на скаляр К матрица В есть

B(I,J)=K*A(I,J)

Мы можем определить умножение матрицы А на вектор-столбец, результатом которого является вектор-столбец E, следующим образом:

E(I)=A(I,1)*D1+A(I,2)*D2+A(I,3)*D3=SUM(K)A(I,K)*D(K)

Элемент столбца, стоящий в I-ой строке, равен произведению элементов I-ой строки матрицы, умноженных на соответствующие элементы столбца. Далее, мы можем вычислить произведение двух матриц А и В.

C(I,J)=A(I,1)*B(1,J)+A(I,2)*B(2,J)+A(I,3)*B(3,J)=SUM(K) A(I,K)*B(K,J), где I<=l, J<=3

Для получения элемента, стоящего в I-ой строке и J-ом столбце, мы вычисляем сумму произведений элементов I-ой строки матрицы А на соответствующие элементы матрицы В. Следует отметить, что произведение матриц необязательно коммутативно, это означает, что произведение А*В не обязательно равно произведению В*А. Например:

но

010		001	010
001	X	010 =	100
100		100	001
001		010	100
010	X	001 =	001
100		100	010

Поупражняйтесь с операциями над матрицами с тем, чтобы владеть этими понятиями в совершенстве.

Среди матриц выделяется так называемая единичная матрица I:

100

I = 010

001

Для каждой матрицы можно вычислить ее детерминант:

DET(A)=A (1,1)*( А (2,2)*А (3,3)-А (2,3)*А (3,2))+А (1,2)*( А (2,3)*А (3,1) — -А(2,1)*А(3,3))+А(1,3)*(А(2,1)*А(3,2)-А(2,2)*А(3,1));

Матрица, у которой детерминант не равен нулю, называется невырожденной, а матрица, у которой детерминант равен нулю, называется вырожденной. Невырожденные матрицы А обладают обратными матрицами А**(-1) такими, что А*(А**(-1))=1. Мы приводим программу (листинг 7.5, глава 7), которая вычисляет обратную матрицу методом сопряженных миноров.

Теперь перейдем к рассмотрению преобразования точек в пространстве. Пусть (X,Y) - координаты точки до преобразования, а (X',Y') - ее координаты после преобразования. Мы определяем преобразование полностью, если задаем формулы для вычисления координаты точек после преобразования по координатам до такового. В случае линейного преобразования, по определению, эта зависимость линейна. Это означает, что правые части уравнений содержат X и Y, умноженные на некоторые множители, и дополнительные константы. Такие уравнения можно написать в виде

X'=A(1,1)*X+A(1,2)*Y+A(1,3) Y'=А (2,1)*Х+A(2,2)*Y+А (2,3)

Значения А называются коэффициентами уравнений. Мы видим, что линейное преобразование получается в результате умножения на коэффициенты значений X, Y и единицы. Мы можем добавить к нашим уравнениям еще одно

I=А(3,1)*Х+A(3,2)*Y+А(3,3)

Так как оно должно выполняться для всех X и Y, то мы пилим, что А(3,1)=А(3,2)=0 и А(3,3)=1. С первого взгляда, кажется, что это не более чем формальная выкладка, но мы позже убедимся в пользе наших рассмотрении. Теперь, если мы представим вектор (X,Y) (который называется вектор-строкой) в виде

X Y I

то приведенные выше три уравнения запишутся в виде умножения столбца на матрицу:

X' А(1,1) А(1,2) А(1,3) X

Y' = А(2,1) А(2,2) А(2,3) = Y

I' А(3,1) А(3,2) А(3,3) I

Таким образом, если мы храним информацию о линейном преобразовании в виде матрицы, то мы можем найти образ каждой точки при преобразовании, если представим ее первоначальные координаты в виде столбца, а затем умножим на эту матрицу.

Многие авторы книг по компьютерной графике предпочитают этому вектору-столбцу вектор-строку (X,Y,I). Тогда преобразование запишется в виде

А(1,1) А(1,2) А(1,3)

(X',Y',I) = (X,Y,I) * А(2,1) А(2,2) А(2,3)

А (3,1) А(3,2) А(3,3)

Обратите внимание, что в этом случае матрица преобразования получается из нашей матрицы А с помощью так называемой операции транспонирования. Этот факт приводит к множеству недоразумений среди тех, кто не знаком с матричным исчислением. Именно поэтому в нашей книге мы придерживаемся обозначений с вектор-столбцами.

Как только вы освоитесь с матрицами получше, вы убедитесь в том, что неплохо переписать некоторые (или все) из программ, составленных ранее, в матричных обозначениях. Неважно, какой из методов применять, важно, что после выбора какого-либо метода следует придерживаться его раз и навсегда (обратите внимание, что матрица В, транспонированная по отношению к А, задается как B(I,J)=A(J,I), где 1<=I,J<=3.

Композиция преобразований Важным свойством матриц является то, что если мы произведем сначала преобразование с матрицей А, а затем преобразование, которому соответствует матрица В, то результирующему преобразованию будет соответствовать матрица С=В*А. Обратите внимание на порядок сомножителей! Такой порядок сомножителей возникает потому, что мы выбрали представление векторов в виде столбцов; если бы представляли вектора строками, то порядок сомножителей был бы более естественным - сначала матрица А, а затем В.

Мы должны написать подпрограмму "MULT2" для умножения двух матриц. Язык бейсик не позволяет передавать векторные переменные в качестве параметров подпрограммы, так что нам придется разработать эффективные методы обхода этого недостатка. Предположим, что все матричные умножения производятся над матрицами А и R с результатом - матрицей В, которая записывается обратно в R. Выбор обозначений и операция копирования станут понятны позже. Нам также потребуется подпрограмма ("IDR2"), присваивающая R значение единичной матрицы. Если нам потребуется вычислить произведение последовательности матриц, то мы вначале положим R=1, а затем каждую матрицу в последовательности справа налево, будем называть А и вызывать подпрограмму "MULT2". По окончании этой процедуры результат произведения последовательности матриц будет храниться в R (см. листинг 4.1) LISTING 4.1

9100 REM MULT2

9101 REM IN - A(3,3)

9102 REM OUT - R(3,3) 9110 FOR I=1 TO 3 9120 FOR J=1 TO 3 9130 LET AR=0

9140 FOR K=1 TO 3

9150 LET AR=AR+A(I,K)*R(K,J)

9160 NEXT K

9170 LET B(I,J)=AR

9180 NEXT J

9190 NEXT I

9200 FOR I=1 TO 3

9210 FOR J=1 TO 3

9220 LET R(I,J)=B(I,J)

9230 NEXT J

9240 NEXT I

9250 RETURN

9300 REM IDR2

9302 REM OUT - R(3,3)

9310 FOR I=1 TO 3

9320 FOR J=1 TO 3

9330 LET R(I,J)=0

9340 NEXT J

9350 LET R(I,I)=1

9360 NEXT I

9370 RETURN

Все естественные преобразования плоскости могут быть представлены в виде произведения трех преобразований: переноса, растяжения и вращения относительно начала координат. Следует подчеркнуть, что матрицы всех этих преобразований невырождены.

Следующие подпрограммы формируют матрицу А для каждого из этих преобразований, что делает возможным использование подпрограммы "MULT2" для того, чтобы составить композицию этих преобразований.

Перенос

Точка с координатами (X,Y) переводится в точку с новыми координатами (X',Y') с помощью вектора (TX,TY):

X'=1*X+0*Y+TX Y'=0*X+1*Y+TY

так что матрица этого преобразования

1 0 ТХ

0 1 TY

0 0 1

Программа "TRAN2" генерирует такую матрицу по заданным значениям параметров ТХ и TY (см. листинг

4.2).

LISTING 4.2

9000 REM TRAN2

9001 REM IN - TX,TY

9002 REM OUT - A (3,3) 9010 FOR I=1 TO 3 9020 FOR J=1 TO 3 9030 LET A(I,J)=0 9040 NEXT J

9050 LET A(I,I)=1 9060 NEXT I

9070 LET A(1,3)=TX: LET A(2,3)=TY 9080 RETURN

Растяжение

При таком преобразовании координата X умножается на SX, а Y-координата точки на SY;

X'=SX*X+0*Y+0 Y'=0*X+SY*Y+0

и соответствующая матрица

SX 0 0

0 SY 0

0 0 1

Обычно SX и SY положительны, но если одно из них отрицательно, то это приводит дополнительно к отражению, в частности если SX=-1 и SY=1, то точка отражается относительно оси Y. Подпрограмма "SCALE2" генерирует матрицу А по заданным значениям X и Y.

LISTING 4.3

8900 REM SCALE2

8901 REM IN - SX,SY

8902 REM OUT - A(3,3) 8910 FOR I=1 TO 3 8920 FOR J=1 TO 3 8930 LET A(I,J)=0 8940 NEXT J

8950 NEXT I

8960 LET A(1,1)=SX: LET A(2,2)=SY: LET A(3,3)=1 8970 RETURN

Вращение относительно начала координат Если поворачиваем плоскость на угол ТЕТА против часовой стрелки (такой способ отсчета является общепринятым в математической литературе) относительно начала координат, то уравнения, определяющие это преобразование, имеют вид:

X'=COS(TETA)*X-SIN(TETA)*Y+0 Y'=SIN(TETA)*X+COS(TETA)*X+0

и матрица:

COS(TETA) -SIN(TETA) 0 SIN(TETA) COS(FKTA) 0 0 0 1

Подпрограмма "ROT2" генерирует матрицу вращения А по заданному значению ТЕТА (см. листинг 4.4) . LISTING 4.4

8600 REM ROT2

8601 REM IN - THETA

8602 REM OUT - A(3,3) 8610 FOR I=1 TO 3 8620 FOR J=1 TO 3 8630 LET A(I,J)=0 8640 NEXT J

8650 NEXT I 8660 LET A(3,3)=1

8670 LET CT=COS THETA: LET ST=SIN THETA 8680 LET A(1,1)=CT: LET A(2,2)=CT 8690 LET A(1,2)=-ST: LET A(2,1)=ST 8700 RETURN

Обратное преобразование Для каждого преобразования имеется преобразование, которое восстановит исходные позиции точек. Если матрице соответствует матрица А, то обратному преобразованию соответствует матрица А**(-1). Если преобразование разложено в композицию элементарных, то нет необходимости в вычислении обратной матрицы использовать подпрограмму на листинге 7.5, мы можем найти ее, используя программы на листингах 4.2, 4.3, 4.4 со значениями параметров, которые вычисляются по значениям соответствующих параметров исходного преобразования.

• Преобразование переноса с (TX,TY) обращается преобразованием переноса с (-TX,-TY);

• Растяжение со значением коэффициентов растяжения SX и SY обращается растяжением со значением коэффициентов 1/SX, 1/SY (ни одно из чисел SX и SY не обращается в нуль, в противном случае двумерное пространство выродилось бы в прямую).

• Поворот на угол ТЕТА обращается поворотом на угол -ТЕТА;

• Если преобразование есть произведение преобразований вращения, переноса и растяжения, например, А*В*С*...*М, то матрица обратного преобразования:

М**(-1)*...*С**(-1)*В**(-1)*А**(-1) Обратите внимание на порядок сомножителей!

Размещение объекта

Нам часто приходится рисовать предмет в различных участках экрана и по разному повернутым. Чрезвычайно неудобно было бы каждый раз вычислять вручную координаты точек предмета, а затем вводить их в программу.

Вместо этого введём сначала произвольную, но фиксированную систему координат, которую мы назовем абсолютной системой координат (ABSOLUTE). Затем мы выбираем наиболее удобную систему координат, в которой мы задаем координаты вершин фигуры; такое положение фигуры мы назовем SETUP.

Используя матрицы, можно преобразовать вершины объекта из положения SETUP в положение ACTUAL (фактическое положение) в системе координат ABSOLUTE. Положение соответствующих линий и областей устанавливается положением вершин фигуры. Матрицу преобразования, переводящую SETUP в ACTUAL, мы всюду в тексте будем обозначать буквой P (иногда у этой буквы будет появляться индекс, с тем чтобы можно было идентифицировать матрицы, относящиеся к различным таким преобразованиям) . Из-за ограничения на передачу векторных параметров подпрограмм, обычно мы не будем генерировать непосредственно P, а будем использовать эту матрицу для модификации R.

Рассматривание объекта Мы ввели метод перемещения предмета по неподвижной координатной системе ABSOLUTE. Предположим, что взгляд наблюдателя направлен в точку X,Y, системы координат ABSOLUTE, а голова наклонена под углом ALPHA. Удобнее полагать, что взгляд направлен на начало координат, а голова не наклонена (такое положение называется OBSERVED - наблюдаемое положение). Таким образом, нам приходится ввести еще одну матрицу Q, переводящую позицию ACTUAL в OBSERVED.

Эта матрица получается комбинацией трансляции точек пространства на вектор (-DX,-DY), которому соответствует матрица A, и последующим поворотом на угол -ALPHA, которому соответствует матрица B (обратите внимание на знак минус!). Так матрица Q=В*А генерируется программой "LOOK2", приведенной на листинге 4.5. Как правило, мы не вычисляем матрицу Q явно, а используем ее только для преобразования матрицы P. Эту матрицу имеет смысл вычислять явно и сохранить в памяти. LISTING 4.5 8200 REM LOOK2

8202 REM OUT - R(3,3)

8210 INPUT "(DX,DY)=";DX;",";DY

8220 INPUT "ALPHA=";ALPHA

8229 REM LOOK AT (DX,DY)

8230 LET TX=-DX: LET TY=-DY 8240 GO SUB TRAN2: GO SUB MULT2

8249 REM TILT HEAD THROUGH ALPHA RADIANS.

8250 LET THETA=ALPHA

8260 GO SUB ROT2: GO SUB MULT2 8270 RETURN

Вычерчивание объекта Комбинируя матрицу преобразования P, переводящую положение SETUP в положение ACTUAL с матрицей Q, переводящей ACTUAL в OBSERVED, получим матрицу R=Q+P, переводящую SETUP в OBSERVED (мы всегда будем обозначать эту матрицу R; следует иметь в виду, что R всегда получается использованием подпрограммы "MULT2"). Преобразовывая все вершины фигуры в положении R и производя соответствующее преобразование линий и областей, мы получим координаты точек фигуры в системе координат наблюдателя, который смотрит в начало системы координат ABSOLUTE и держит голову вертикально, то есть такого наблюдателя, который смотрит на экран.

Таким образом, мы отождествляем систему координат ABSOLUTE с системой, соответствующей полю экрана для определения координат точек фигуры на графическом поле экрана с тем, чтобы нанести на экран вершины, прямые и области, из которых состоит объект. На практике это достигается с помощью конструирующей подпрограммы, использующей матрицу R. Эта подпрограмма установит необходимую информацию о вершинах фигуры, линиях и областях, преобразует вершины с помощью матрицы R, а затем, возможно, нарисует объект (см. пример 4. А).

Позже мы увидим, что существуют ситуации, в которых удобнее сохранить в памяти информацию о вершинах, линиях и областях фигуры. Например, координаты вершин могут храниться в одномерных массивах X и Y; информация о прямых - в двумерном массиве I. Координаты вершин могут запоминаться в положении исходное, фактическое, или наблюдаемое - это зависит от программы. Этот метод используется для создания динамической последовательности сцен: объекты могут перемещаться относительно системы координат абсолютно, относительно самих себя и, кроме того, обозреватель может перемещаться по экрану. Рассмотрим вначале простейший случай неподвижного изображения.

Сложные изображения - метод построения изображения "по кирпичикам" У нас есть метод, позволяющий генерировать последовательность подобных изображений объекта. Для этого достаточно создать программу, рисующую объект, а затем вызывать ее с различными значениями матрицы P, соответствующей преобразованию из исходного положения в наблюдаемое. Изображение создается подпрограммой "SCENE2", которая вызывается из стандартной главной программы (см. листинг 4.6). Эта главная программа используется для установления меток различных подпрограмм, объявляет массивы, устанавливает значения параметров VERT и HORIZ, а затем вызывает подпрограмму "SCENE2". LISTING 4.6

100 REM MAIN PROGRAM

109 REM Define identifiers for initialisation and 2-D PLOT routines.

110 LET START=9700: LET SETORIGIN=9600: LET MOVETO=9500: LET LINETO=9400: LET CLIP=8400

120 LET ROT2=8600: LET ANGLE=8800: LET SCALE2=8900: LET TRAN2=9000: LET MULT2=9100: LET IDR2=9300

130 LET SCENE2=6000: LET LOOK2=8200

139 REM INITIALISE AND CENTRE GRAPHICS AREA.

140 INPUT "HORIZ=";HORIZ;",";"VERT=";VERT 150 GO SUB START

160 LET XMOVE=HORIZ*0.5: LET YMOVE=VERT*0.5 170 GO SUB SETORIGIN

179 REM SET THE SCENE.

180 GO SUB SCENE2 190 STOP

"SCENE2" сначала вызовет "LOOK2" и вычислит матрицу Q, и если ей предстоит начертить более одной фигуры, то эта матрица заносится в память. Для каждого отдельного элемента ("кирпичика") мы вычисляем матрицу P и затем вызываем необходимую подпрограмму построения изображения, используя R=Q+P. В итоге из кирпичиков выстраивается необходимая картинка. Для того, чтобы различать матрицы, относящиеся к разным элементам, мы добавляем индексы.

Может быть, предложенный нами модульный подход к решению и не является самым эффективным, но наш опыт показывает, что этот метод чрезвычайно проясняет решение для начинающих и позволяет им задавать правильные вопросы о процессе построения того или иного объекта. Мы увидим, что при мультиплицировании изображения наш подход позволяет уменьшить количество подзадач, так как в этом случае не только элементы перемещаются относительно друг друга, но и движется наблюдатель.

Естественно, что если считать, что наблюдатель держит голову вертикально, то вычисление матрицы можно свести к обращению к подпрограмме "SETORIGIN" (установить начало), которая изменяет положение начала координат системы координат, связанной с экраном. Если наблюдатель смотрит на начало координат и его голова вертикальна, то матрица Q равна 1; в этом случае она не принимает участия в генерации изображения и тогда подпрограммой "LOOK2" можно пренебречь. Однако, мы будем иметь дело с общим случаем. Мы ставим своей целью объяснить понятие преобразования пространства в наиболее общем случае, используя самые прямые методы, несмотря на то, что это может потребовать от читателя больших усилий при чтении. К этим подпрограммам следует возвращаться по мере изучения книги. Позже мы наметим пути изменения этих программ так, чтобы они были эффективными в конкретных приложениях.

Однако основная причина использования модульного метода построения программ станет понятной при изучении трехмерной графики. Перед тем как изучать методы трехмерной графики, следует хорошо изучить двухмерную графику, так как многие методы являются общими для этих случаев.

Пример 4.А

Рассмотрим простейшее изображение космического корабля, который в исходном положении направлен параллельно оси X. Контур корабля получается последовательным соединением точек (3,0), (0,0), (-1,1), (2,0), (-1,-1) и снова (0,0). См. рис. 21, на котором изображен корабль; размеры графического поля 5 блоков на 3 блока, а матрица, переводящая исходное положение в фактическое, единичная. Матрица, соответствующая преобразованию исходное в наблюдаемое, такова, что взгляд наблюдателя направлен в точку (1,0), а его голова вертикальна.

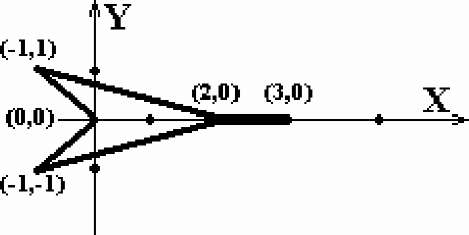
На листинге 4.7 приведена подпрограмма "SCENE2" в том виде, в каком она необходима для установки объекта в правильное положение; на листинге 4.8 приведена подпрограмма, вычерчивающая контуры корабля.

Обратите внимание, что подпрограмма "SHIP", которая использует матрицу P для перемещения вершин корабля (а следовательно, и самого корабля) в положение координат последних, а вместо этого сохраняются значения Х(6), Y(6) с тем, чтобы можно было вызывать подпрограмму повторно для генерации изображения в других положениях.

LISTING 4.7

6000 REM SCENE2/LOOK2 - SHIP (NOT STORED) 6010 DIM X(6):DIM Y(6)

6020 DIM A(3,3): DIM B(3,3): DIM R(3,3) 6030 LET SHIP=6500

6039 REM PLACE THE OBSERVER.

6040 GO SUB IDR2: GO SUB LOOK2

6049 REM DEFINE AND DRAW OBJECT.

6050 GO SUB SHIP 6060 RETURN LISTING 4.8

6500 REM SHIP/ NOT STORED

6501 REM IN - R(3,3)

6510 DATA 3,0,0,0,-1,1,2,0,-1,-1,0,0 6520 RESTORE SHIP 6530 FOR I=1 TO 6

6539 REM READ COORDINATES OF SETUP OBJECT.

6540 READ XX,YY

6549 REM MOVE OBJECT INTO OBSERVED POSITION.

6550 LET X(I)=XX*R(1,1)+YY*R(1,2)+R(1,3) 6560 LET Y(I)=XX*R(2,1)+YY*R(2,2)+R(2,3) 6570 NEXT I

6579 REM JOIN VERTICES IN ORDER.

6580 LET XPT=X(1): LET YPT=Y(1): GO SUB MOVETO 6590 FOR I=2 TO 6

6600 LET XPT=X(I): LET YPT=Y(I): GO SUB LINETO 6610 NEXT I 6620 RETURN

Пример 4. Б

Предположим, что мы хотим начертить рисунок, состоящий из четырех космических кораблей A, B, C, D, размещенных на экране 60х40. Для простоты мы полагаем, что Q - единичная матрица, так что голова наблюдателя вертикальна, а взгляд направлен в начало координат.

Корабль A расположен так же, как и в положении исходное; это означает, что R(A)=1, в то время как корабль B переводится из положения исходное в фактическое с помощью следующих преобразований:

1. 2. 3.

Фигура растягивается; параметры растяжения X=4, Y=2; соответствует этому преобразованию матрица A; Фигура поворачивается на PI/6 радиан матрицей B;

Производится параллельный перенос с параметрами ТХ=6, TY=4 - матрица C.

	4	0	0	SQRT (3)	1	0
A	= 0	2	0	2	2
	0	0	1
	1	0	6	B = 1	SQRT (3)	0
				2	2
С	=0	1	4
	0	0	1	0	0	1

Результирующее преобразование задается матрицей

R(B)=Q*P(B)=I*P(В)=Р(В)=С*В*А

Обратите внимание на то, как используется нижний индекс для указания того, что матрица относится к элементу B.

Если мы используем другой порядок сомножителей A*B*C (что дает матрицу P), тогда

2* SQRT (3) -1 6 2* SQRT (3) - 2 12* SQRT (3) - 8

SQRT (3) 4 P(D) = 1 SQRT (3) 4* SQRT (3) + 6

P(B) = 2 0

откуда видно, что мы пришли к совершенно другому преобразованию. Матрице P(D)=Q*P(D)=I*P(D) соответствует корабль D. Обратите внимание, что корабль ассиметричен; пользуясь операцией растяжения, следует помнить, что она определена относительно начала координат. Так что форма предмета, который удален от начала координат, может быть искажена.

Корабль C получается из корабля B отражением относительно прямой 3*Y=-4*X-9. Эта прямая пересекает ось Y в точке (0,3) и образует с положительной полуосью X угол GAMMA

GAMMA=ARCCOS(-3/5)=ARCSIN(4/5)=ARCTG(-3/4) Если мы совершим параллельный перенос на вектор (0,3), которому соответствует матрица D, то эта прямая пройдет через начало координат; если мы повернем плоскость на угол ALPHA матрицей E, то наша прямая совпадет с осью X. Матрица F тогда отразит корабль относительно оси X, матрица E**(-1) повернет прямую так, что она снова будет составлять угол с осью X, и матрица D**(-l) вернет прямую в исходное положение. Таким образом, матрица G=d**(-1)*E**(-1)*F*E*D отражает вершины корабля относительно прямой 3*Y=-4*X-9 и R(C)=I*P©=G*P(B) может использоваться для генерации изображения C, что означает, что мы сначала матрицей P устанавливает корабль в положение B, а затем матрицей G в положение C.

3 4^ -0 5 5

E= -- -- 0 55

0 0 1

Г- 48 -14* SQRT (3) 7 - 24* SQRT (3) - 210 ^

1 0

F = 0 -1 00

0 0 1

R(C) =

-14 - 48* SQRT (3) 24

7* SQRT (3) -170 25

_v ----у

На листинге 4.9 приведена новая программа для рисования нашей фигуры. Обратите внимание, что "SCENE2" не вызывает "LOOK2", так как мы полагаем, что взгляд наблюдателя направлен на начало координат, и голову он держит прямо. Основная программа и подпрограмма "SHIP", а также все остальные графические подпрограммы остаются неизменными.

LISTING 4.9

6000 REM SCENE2/NO LOOK2 4 SHIP (NOT STORED).

6010 DIM X(6): DIM Y(6)

6020 DIM A(3,3): DIM B(3,3): DIM R(3,3)

6030 LET SHIP=6500

6038 REM OBSERVED=ACTUAL. NO NEED TO CALL "LOOK2".

6039 REM SHIP A.

6040 GO SUB IDR2: GO SUB SHIP

1 0 0 D = 0 1 3 0 0 1

6049 REM SHIP B.

6050 LET SX=4: LET SY=2

6060 GO SUB SCALE2: GO SUB MULT2

6070 LET THETA=PI/6

6080 GO SUB ROT2: GO SUB MULT2

6090 LET TX=6:LET TY=4

6100 GO SUB TRAN2: GO SUB MULT2

6110 GO SUB SHIP

6119 REM SHIP C.

6120 LET AX=-3:LET AY=4 6130 GO SUB ANGLE

6140 LET TX=0:LET TY=3

6150 GO SUB TRAN2: GO SUB MULT2

6160 LET THETA=-THETA

6170 GO SUB ROT2: GO SUB MULT2

6180 LET SX=1: LET SY=-1

6190 GO SUB SCALE2: GO SUB MULT2

6200 LET THETA=-THETA

6210 GO SUB ROT2: GO SUB MULT2

6220 LET TX=0: LET TY=3

6230 GO SUB TRAN2: GO SUB MULT2

6240 GO SUB SHIP

6249 REM SHIP D.

6250 GO SUB IDR2

6260 LET TX=6: LET TY=4

6270 GO SUB TRAN2: GO SUB MULT2

6280 LET THETA=PI/6

6290 GO SUB ROT2: GO SUB MULT2

6300 LET SX=4:LET SY=2

6310 GO SUB SCALE2: GO SUB MULT2

6320 GO SUB SHIP

6330 RETURN

Упражнение 4.1

Для того, чтобы убедиться, что программу можно использовать в общей ситуации, пропустите эту программу с матрицей Q, отличной от единицы, что достигается ненулевым значением DX, DY или ALPHA.

Ваша программа "SCENE2" должна вызывать "LOOK2" для вычисления Q, которая хранится в памяти. Затем для каждого объекта на экране вычисляется матрица P перехода из исходного положения в фактическое (эта матрица хранится подпрограммой "MULT2" в R), умножается на матрицу Q, которая копируется в матрицу A для использования в подпрограмме "MULT2", а затем вызывается подпрограмма построения с матрицей R=Q+P.

Используйте подпрограмму "LINETO", которая вызывает подпрограмму "CLIP", так как в противном случае при вычерчивании участков фигур, выходящих за графическое поле, произойдет сбой программы. Упражнение 4.2

Используйте предыдущие подпрограммы для вычерчивания фигур кораблей, но числа, положение и направление кораблей вводится с клавиатуры. Вы можете написать свои подпрограммы для генерирования более сложных изображений; мы выбрали очень простую картинку, так как не хотели усложнять алгоритм сложностью самих объектов.

Этим методом можно манипулировать с любым числом точек и линий, которыми может справиться SPECTRUM с учетом ограничений на память и время. Объекты могут быть не просто состоящими из линий, но и имеющими разноцветные участки (многоугольники, вершины которых являются преобразованными точками). Упражнение 4.3

Используя циклы, можно генерировать последовательности объектов, например, они могут быть одинаково направлены, а их центры расположены на прямой P+MU*Q на одинаковом расстоянии друг от друга.

Мы можем генерировать значения MU с помощью цикла и рисовать по одному кораблю на каждом шаге; при этом мы можем изменять параметры преобразования регулярным образом, используя MU, P и Q.

Эти новые значения параметров используются для вычисления матрицы преобразования из исходного положения в фактическое на каждом шаге, передвигая таким образом объект в новое положение. R=Q*P=I*P используется для наблюдения за объектом и для его вычерчивания. Используя эти идеи, нарисуйте картины боев между кораблями.

Эффективное использование матриц Очевидно, что какую бы мы комбинацию преобразований ни использовали, третьей строкой матрицы всегда будет (0,0,1). Если мы будем использовать только две верхних строки, то это сделает нашу подпрограмму значительно более эффективной.

Мы продолжаем хранить матрицы 3x3, так как процедуры, написанные нами ранее, используют матрицы 3x3. Изменение размерности массивов привело бы к нарушению границ массивов в предыдущих подпрограммах - лишние три столбца, добавленные к каждой матрице; это малая цена, которую мы платили, чтобы избежать ошибки.

Обратите внимание, что когда мы объявляем массив оператором DIM, то элементам массива присваивается нулевое значение. Перепишем с учетом этого обстоятельства, подпрограммы на листингах 4.1, 4.2, 4.3, 4.4 и обозначим их 4.1A, 4.2A, 4.3A, 4.4A соответственно.

LISTING 4.1 A
9100	REM MULT2
9101	REM IN - A(3,3),R(3,3)
9102	REM OUT - R(3,3)
9110	FOR I=1 TO 2
9120	FOR J=1 TO 3
9130	LET B(I,J)=A(I,1)*R(1,J)+A(I,	2)*R(2,J)
9140	NEXT J
9150	LET B(I,3)=B(I,3)+A(I,3)
9160	NEXT I
9170	FOR J=1 TO 3
9180	LET R(1,J)=B(1,J): LET R(2,J)	=B(2,J)
9190	NEXT J
9200	RETURN
9300	REM IDR2
9302	REM OUT - R(3,3)
9310	DIM R(3,3)
9320	LET R(1,1)=1: LET R(2,2)=1
9330	RETURN
LI STING 4.2 A
9000	REM TRAN2
9001	REM IN - TX,TY

9002 REM OUT - A(3,3) 9010 DIM A(3,3)

9020 LET A(1,1)=1: LET A(2,2)=1: LET A(1,3)=TX: LET A(2,3)=TY 9030 RETURN LISTING 4.3 A

8900 REM SCALE2

8901 REM IN - SX.SY

8902 REM OUT - A(3,3) 8910 DIM A(3,3)

8920 LET A(1,1)=SX: LET A(2,2)=SY 8930 RETURN LISTING 4.4A

8600 REM ROT2

8601 REM IN - THETA

8602 REM OUT - A(3,3) 8610 DIM A(3,3)

8620 LET CT=COS THETA: LET ST=SIN THETA 8630 LET A(1,1)=CT: LET A(2,2)=CT 8640 LET A(1,2)=ST: LET A(2,1)=ST 8650 RETURN

Может показаться, что пример с нашими кораблями несколько надуман, так как координаты объектов выбраны произвольно. Однако при построении большинства диаграмм положение объектов определяется явным образом, исходя из строения диаграммы (см. приведенные ниже примеры).

Пример 4. В

Напишите программу, которая чертит эллипс с главными осями A и B и центром в точке (CX,CY). Большая ось образует с осью X угол TETA.

Обратите внимание на то, что порядок операций здесь существенен: сначала поворачивайте, а затем переносите. Если мы хотим генерировать эллипсы с горизонтальной главной осью, то мы можем не использовать матрицы, используя подпрограмму упражнения 2.5 и методы подпрограмм на листинге 2.9.

На листинге 4.10 приводится подпрограмма "SCENE2", которая считывает информацию об эллипсе, вычисляет матрицу преобразования исходного положения в фактическое, а затем вызывает подпрограмму "ELLIPCE" для вычерчивания эллипса (см. рис.22).

Рис. 22.

LISTING 4.10

6000 REM SCENE2/ELLIPSE

6010 DIM A(3,3): DIM B(3,3): DIM R(3,3) 6020 LET ELLIPSE=6500

6030 INPUT "(CX,CY)=";CX;",";CY;" A=";A;" B=";B;" THETA=";THETA 6040 LET THETA=-THETA

6049 REM Ellipse centred at (CX,CY) and tilted through angle THETA.

6050 GO SUB IDR2

6060 GO SUB ROT2: GO SUB MULT2 6070 LET TX=CX: LET TY=CY 6080 GO SUB TRAN2: GO SUB MULT2 6090 GO SUB ELLIPSE 6100 RETURN

6500 REM ELLIPSE

6501 REM IN - A,B,R(3,3)

6509 REM ELLIPSE. MAJOR AXIS A. MINOR AXIS B.

6510 LET XPT=A*R(1,1)+R(1,3) 6520 LET YPT=A*R(2,1)+R(2,3) 6530 GO SUB MOVETO

6540 LET ALPHA=0: LET ADIF=PI/100

6549 REM Calculate points (XPT.YPT) on ellipse, in observed position.

6550 FOR I=1 TO 200

6560 LET ALPHA=ALPHA+ADIF

6570 LET AA=A*COS ALPHA: LET BB=B*SIN ALPHA

6580 LET XPT=AA*R(1,1)+BB*R(1,2)+R(1,3)

6590 LET YPT=AA*R(2,1)+BB*R(2,2)+R(2,3)

6600 GO SUB LINETO

6610 NEXT I

6620 RETURN

Упражнение 4.4

Напишите подпрограмму, рисующую единичный перемещаемый объект, а затем используйте матричную технику для составления комбинаций этих объектов. Для примера возьмите следующую фигуру, заданную в параметрической форме:

(R(COS(TETA)**3)/(SIN(TETA)**3)),

где 0<=ТЕТА<=2*PI, а R - радиус (максимальное расстояние точки на кривой до начала координат)

Параметры, необходимые для работы этой подпрограммы - это радиус R и матрица преобразования. Упражнение 4.5

Поэкспериментируйте с этой матричной техникой. Напишите подпрограмму, которая поворачивает плоскость относительно точки (X,Y) на угол ТЕТА. Напишите программу, которая осуществляет отражение плоскости относительно прямой A*Y=B*X+C.

Хранение информации об изображении Ранее мы упоминали, что иногда приходится запоминать всю информацию об изображении перед тем, как выйти из подпрограммы построения изображения. В этом случае информация хранится в одномерных массивах X и Y длины большей или равной NOV, где NOV - количество вершин, которые необходимо запомнить (эти точки могут соответствовать позиции SETUP, ACTUAL или OBSERVED, все зависит от контекста). Нам также потребуется хранить информацию о прямых, в двумерном массиве которого первый индекс изменяется от 1 до 2, а второй изменяется от 1 до величины, большей или равной NOL, где NOL - количество прямых в изображении. I-ая прямая соединяет точки с индексами L(1,I) и L(2,I); мы видим, что эта информация зависит от предыдущей, она просто сообщает нам номера точек, которые соединяет I-ая прямая. Значениям параметров NOV и NOL присваиваются начальные значения в подпрограмме "SCENE2" и увеличиваются подпрограммами построения изображения.

Теперь мы можем в программах построения изображения не чертить прямые, а использовать их только для записи в память информации о вершинах, прямых и т.д. (преобразованных матрицей R). После того как вся информация об изображении записана в память подпрограммой "SCENE2", вызывается подпрограмма "DRAWIT" ("РИСУЙ"), которая и вычерчивает изображение. Программа для создания изображения наших кораблей, использующая новый метод, получается из подпрограммы на листинге 4.9 внесением трех небольших изменений: 6010 DIM X(20): DIM Y(20): DIM L(2,20)

6030 LET NOV=0: LET NOL=0: LET SHIP=6500: LET DRAWIT=7000 6330 GO SUB DRAWIT: RETURN

Эта подпрограмма используется вместе с листингом 4.11, где имеется текст подпрограммы, записывающей информацию об изображении и рисующую подпрограмму.

LISTING 4.11

6500 REM SHIP/STORED

6501 REM IN - NOV,NOL,R(3,3),X(NOV),Y(NOV)

6502 REM OUT - NOV,NOL,X(NOV), Y(NOV),L(2,NOL)

6510 DATA 3,0,0,0,-1,1,2,0,-1,-1,1,2,2,3,3,4,4,5,5,2

6520 RESTORE SHIP 6530 LET NV=NOV

6539 REM Read vertices and move into position using matrix R.

6540 FOR I=1 TO 5 6550 READ XX,YY 6560 LET NOV=NOV+1

6570 LET X(NOV)=XX*R(1,1)+YY*R(1,2)+R(1,3) 6580 LET Y(NOV)=XX*R(2,1)+YY*R(2,2)+R(2,3) 6590 NEXT I

6599 REM READ AND STORE LINE INFORMATION.

6600 FOR I=1 TO 5 6610 READ L1,L2 6620 LET NOL=NOL+1

6630 LET L(1,NOL)=L1+NV: LET L(2,NOL)=L2+NV 6640 NEXT I 6650 RETURN

7000 REM DRAWIT

7001 REM IN - NOV,X(NOV),Y(NOV),NOL,L(2,NOL)

7009 REM DRAW LINE BY JOINING PAIRS OF VERTICES.

7010 FOR I=1 TO NOL

7020 LET L1=L(1,I): LET L2=L(2,I)

7030 LET XPT=X(L1): LET YPT=Y(L1): GO SUB MOVETO 7040 LET XPT=X(L2): LET YPT=Y(L2): GO SUB LINETO 7050 NEXT I 7060 RETURN

Предположим, что мы хотим создать несколько видов одной и той же картины (мы опять используем в качестве примера наш космический корабль); это означает, что при той же матрице преобразования P SETUP в ACTUAL, но с различными матрицами Q преобразования из ACTUAL в OBSERVED. Очевидное решение этой задачи - записать в память информацию о вершинах в положении ACTUAL.

Теперь для каждого нового положения OBSERVED мы вычисляем Q и вводим это значение в другую подпрограмму "DRAWIT" (см. листинг 4.12, который отличается от листинга 4.11), которая переводит каждую вершину из положения ACTUAL в OBSERVED с помощью матрицы Q, записывает координаты этих вершин в массивы V и W и использует эти значения, когда они требуются для генерации изображения. Когда мы используем этот метод создания изображения, мы изменяем только подпрограммы "SCENE2" и "DRAWIT" и то лишь слегка (см.

листинг 4.12).
LISTING 4.12
6000	REM SCENE2/VARIABLE LOOK2. 4 SHIPS (STORED).
6009	REM CONSTRUCT 4 SHIPS STORED IN	ACTUAL POSITION
6010	DIM X(20): DIM Y(20): DIM V(20):	DIM W(20): DIM
6020	DIM A(3,3): DIM B(3,3): DIM R(3,	3)
6030	LET SHIP=6500: LET DRAWIT=7000
6039	REM SHIP A.
6040	LET NOV=0:LET NOL=0: GO SUB IDR2	: GO SUB SHIP
6049	REM SHIP B.
6050	LET SX=4: LET SY=2
6060	GO SUB SCALE2: GO SUB MULT2
6070	LET THETA=PI/6
6080	GO SUB ROT2: GO SUB MULT2
6090	LET TX=6:LET TY=4
6100	GO SUB TRAN2: GO SUB MULT2
6110	GO SUB SHIP
6119	REM SHIPC.
6120	LET AX=-3:LET AY=4
6130	GO SUB ANGLE
6140	LET TX=0:LET TY=3
6150	GO SUB TRAN2: GO SUB MULT2
6160	LET THETA=-THETA
6170	GO SUB ROT2: GO SUB MULT2
6180	LET SX=1:LET SY=-1
6190	GO SUB SCALE2: GO SUB MULT2
6200	LET THETA=-THETA
6210	GO SUB ROT2: GO SUB MULT2
6220	LET TX=0:LET TY=-3
6230	GO SUB TRAN2: GO SUB MULT2
6240	GO SUB SHIP
6249	REM SHIP D.

6250 GO SUB IDR2

6260 LET TX=6:LET TY=4

6270 GO SUB TRAN2: GO SUB MULT2

6280 LET THETA=PI/6

6290 GO SUB ROT2: GO SUB MULT2

6300 LET SX=4:LET SY=2

6310 GO SUB SCALE2: GO SUB MULT2

6320 GO SUB SHIP

6329 REM LOOP THROUGH OBSERVATION POINTS.

6330 GO SUB IDR2: GO SUB LOOK2 6340 CLS: GO SUB DRAWIT

6350 GO TO 6330 6360 RETURN

7000 REM DRAWIT

7001 REM IN - NOV,NOL,R(3,3),X(NOV),Y(NOV),L(2,NOL)

7009 REM Transform vertices from actual to observed position.

7010 FOR I=1 TO NOV

7020 LET V(I)=X(I)*R(1,1)+Y(I)*R(1,2)+R(1,3) 7030 LET W(I)=X(I)*R(2,1)+Y(I)*R(2,2)-R(2,3) 7040 NEXT I

7049 REM DRAW LINES BY JOINING PAIRS OF VERTICES.

7050 FOR I=1 TO NOL

7060 LET L1=L(1,I): LET L2=L(2,I)

7070 LET XPT=V(L1): LET YPT=W(L1): GO SUB MOVETO 7080 LET XPT=V(L2): LET YPT=W(L2): GO SUB LINETO 7090 NEXT I 7100 RETURN Упражнение 4.6

Создайте движущиеся изображения. Каждая новая сцена изображает плывущие относительно друг друга корабли. Движение кораблей должно задаваться каким-нибудь удобным образом. Наблюдатель тоже должен двигаться; например, в начальный момент времени взгляд наблюдателя направлен в начало координат, затем, через пять кадров, он смотрит в точку (10,10) и с каждым новым кадром голова наклоняется на 0.1 радиан.

Теперь у вас нет необходимости вводить значения (DX,DY) и ALPHA в подпрограмму "LOOK2", вместо этого они вычисляются в программе. После того, как вы прочитаете главу 13, вы сможете поместить эти пять сцен в память, а затем извлекать их с помощью подпрограммы "MOVIE" ("мультипликация"), если у вас 48-ми килобайтовый вариант SPECTRUMa.

Упражнение 4.7

Сгенерируйте диаграматизированное изображение комнаты, в которой вы живете - двумерное схематическое изображение столов, стульев и т. д. Различные типы предметов используют различные программы генерации изображения, и "SCENE2" должна считывать информацию о предметах в комнате. Как только ваша комната воссоздана в машинной форме, сгенерируйте последовательность видов вашей комнаты, которые получаются различными выборами места обзора и направления взгляда.

Вы можете пойти другим путем и сначала нарисовать схему ее под разными углами. Выбор различных сцен огромен!

Так как мы используем "CLIP" в подпрограмме "LINETO", то мы можем задавать небольшие значения HORIZ и VERT, что производит эффект "зума" - визуального увеличения участка схемы, при этом внешности участка прямых будут обрезаны.

Список программ

Мы сгруппируем листинги 3.4 (ANGLE-угол), 4.1A ("MULT2" и "IDR2"), 4.2A ("TRAN2"), 4.3A ("SCALE2"), 4.4A ("ROT2"), 4.5 ("LOOK2") и 4.6 ("MAIN PROGRAM") подзаголовком "LIB2".

1. "LIB1", "LIB2", листинг 4.7 ("SCENE2") и 4.8 "SHIP". Необходимая входная информация: HORIZ, VERT, DX, DY и ALPHA. Попробуйте значения 8, 5, 1, 1, 0.5. Зафиксируйте четыре из этих значений и изменяйте пятое небольшими шагами.

2. "LIB1", "LIB2", листинг 4.9A ("SCENE2") и 4.8 ("SHIP"). Входные данные: HORIZ, VERT. Попробуйте 30, 20, 60, 40.

3. "LIB1", "LIB2" и листинг 4.10 ("SCENE2EL"). Входные данные: HORIZ, VERT, СХ, CY, А, В, ТНЕТА. Попробуйте 30, 20, 0, 0, 12, 9, 0. Снова зафиксируйте значения параметров, кроме одного, и медленно изменяйте значения оставшегося параметра.

4. "LIBI", "LIB2", листинги 4.9A (вариант "SCENE2N") и 4.11 ("SHIP" и "DRAWIT"). Входные данные: те же, что и в пункте 2.

5. "LIBI", "LIB2", листинги 4.11 ("SHIP") и 4.12 ("SCENE2" и "DRAWIT"). Входные данные: HORIZ, VERT, DX, DY, ALPHA. Попробуйте значения: 60, 40, 0, 0, 0. Последовательно изменяйте значения переменных.

СОДЕРЖАНИЕ:

Темы: Игры, Программное обеспечение, Пресса, Аппаратное обеспечение, Сеть, Демосцена, Люди, Программирование