УРОК 8

8. 1 Вступление.

выше мы уже показали, что компьютеры могут служить не
только для работы с числами, но теперь уже настал момент и для
того, чтобы поговорить об обработке чисел. Ны сконцентрируемся
на довольно простой арифметике и уверены, что этот раздел будет
вам понятен вне зависимости от уровня вашей предшествующей
подготовки.

8. 2 Арифметическое среднее.

Сколько времени у вас заняла проработка каждого урока в
этой книге? "В среднем, примерно три часа." - ответите вы. Если
Вас спросить о том. сколько времени занимает Ваша дорога на
работу (в школу . в институт), то Вы ответите примерно в том же
духе, любители спорта знают, что такое среднее число голов,
забитых любимой командой в одном матче. Ны можем даже говорить
о средней опенке по Физике в четверти или о среднем возрасте
группы людей.

Если нам надо вычислить среднее значение (арифметическое
среднее) возрастов группы людей, мы сложим возраста всех членов
группы и разделим на количество людей, входящих в эту групцу.
итак, вычисление арифметического среднего происходит в три

этапа:

- сложение:

- пересчет;

- деление результата сложения на результат пересчета.

Найти арифметическое среднее следующих чисел:
6,7,2.5.4.4.9. 8.

Найдем сумму чисел: 6+7+2+5+4+4+9+8 = 45.
всего чисел: 8

Среднее арифметическое: 45/8=5.625

Найдите среднее арифметическое следующего ряда
чисел: 8,4,2,6,1,7,6,1,4.

програнну для
для следующей

Разработать алгоритм и написать
отыскания среднего арифметического
группы чисел:

56. 47. 52. 65. 24. 34. 59, 37, 49, 66,
38, 24, 62, 76. 31. 47, 66. 61. 74, 45,
66. 44, 55. 67, 36. 56. 54. 54. 50, 43.
18, 83, 23. 79, 29, -9999

Начало работы.
Установим счетчик в 1.
Сумму установим в о.
Ввод очередного числа.

Проверка, не равно ли оно -9999. Если да, то переход на
п. 9. если нет, то на п. 6.

Прибавляен к "сунне" значение очередного числа.
Увеличиваем счетчик на 1.

Возвращаемся на п. 4 для ввода очередного числа.
Берем значение счетчика и уменьшаем его на 1, т.к.
последний раз он был увеличен Зря.

Рассчитываем среднее ариФнетическое. разделив значение
"накопленной" суммы на показания счетчика.
Печать результата.

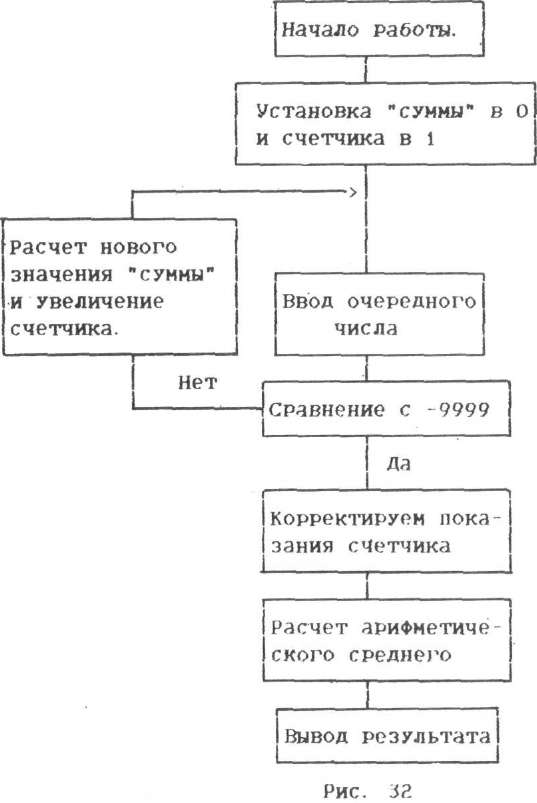
По данной блок-схеме ны уже можем написать програнну:

Програнна 8. 1
£0 PRIHT "Расчет среднего" ариФнетического.
30 LET С=1
40 LET S=0

50 REH ««Главный пикл«»
60 READ Ш

70 IF m=-9999 THEN GO TO 120
80 LET s=s+m
90 LET C = C + 1
100 GO TO 50

110 REH и»»»»»»»»»»»»»»»»»*»»»»»»»
120 REH ««Корректируен счетчик»»
130 LET n=Cl

140 REH x»»»»*»»»»»»»*»»*»»»*»»»*
150 PRIHT

160 PRIHT "Среднее = ";s/n
170 STOP

180 REH I*»»»»*»»»»»»»*»»»»»»»»»»»
190 REH »*Data««

200 DATA 56, 47. 52, 65, 24. 34, 59, 37, 49. 66
210 DATA 38,24.62.76.31.47,66.61.74.45
220 DATA 66, 44, 55. 67. 36, 56, 54. 54. 50. 43
230 DATA 18.83.23.79.29, -9999
240 RUN

Обратите внимание, что в этой программе мы вводили данные
с помошью READ. . . DATA. Вы знаете, что это же можно делать и с
помошью INPUT. Во многих случаях это удобнее. В частности, тог-
да. когда Вы при написании программы еше не знаете, какие дан-
ные будут вводиться. Пример программы со вводом через INPUT
показан ниже.

Программа 8. 2

20 PRINT "Расчет среднего арифметического"

30 LET с=о

40 LET S-0

60 INPUT "Введите число "; п

70 IF 11=-9999 THEN GO ТО 110

75 REH »«с - счетчик введенных чисел»»

80 LET С=С+1

85 REM »«s - сумма введенных чисел»»

90 LET s=s+n

100 GO ТО 50

110 REM »«Среднее««

120 LET a-s/c

130 PRINT "Всего введено "; с

Напишите программу для того, чтобы найти сред-
нюю длину слова в предложении, рссмотренном

нами в ПРИНЕРЕ-5. 2.

УПРАЖНЕНИЕ-8. 2

напишите программу для вычисления средних ре-
зультатов эксперимента по бросанию игровой
Эксперимент тоже поставьте программно, посред-

кости 100 раз.
ством моделирования.

Ноделирование.

Ожидаемое среднее значение результата многократного броса-
ния игровой кости равно:

(1+2+3+4+5+6)/б = 21/6 = 3.5

Мы произвели 3000 бросков (30 серий по 100) и только один
раз получили арифметическое среднее, равное точно 3.5. В ос-
тальных случаях разброс значений составлял от 3. 24 до 3.76.
Что же из этого следует? Ножет быть, сбоит генератор случайных
чисел, недаром их называют псевдослучайными? И еше вопрос,
сколько экспериментов надо поставить, чтобы понять сбоит он или
нет?

Чтобы исследовать эти вопросы досконально, нам пришлось бы
углубиться в дебри математической статистики, а мы себе этого
пока позволить не можем. Но зато мы можем, по крайней мере най-
ти среднее значение полученных средних значений. Для этого надо
всего лишь 30 раз запустить программу и исследовать полученные
результаты:

3. 56; 3. 47; 3. 52; 3. 65; . . .

введем их в вышеприведенную Програмну-8.1 и посмотрим, че-
му равно среднее значение средних значений. Чтобы упростить за-
дачу по вводу длинной последовательности десятчных дробей, мы
вводим только дробную часть:

56, 47, 52. 65. 24. 34. 59. 37. 49.66.
38. 24. 62. 76. 31, 47, 66. 61, 74. 45.
66. 44, 55, 67, 36. 56, 54, 54, 50, 43,
-9999

В итоге получили арифметическое среднее:
3. 51266667

Таким образом, округленно арифметическое среднее по ре-
зультатан 3000 бросков равно 3.51, что довольно близко к пред-
сказанному теорией результату.

Итоги модельного эксперимента.

"Модельный эксперимент" - это, пожалуй, слишком громкие
слова для того, что мы только что сделали. Тем не менее, мы
хотели только подчеркнуть и подчеркнули, что многие события
реальной жизни Вы можете промоделировать на своем компьютере
даже и без углубления в математическую статистику. Так, в на-
турном эксперименте довольно трудоемко и скучно бросать кость
3000 раз, а компьютеру сделать это ничего не стоит, он для того
и нужен, чтобы очень быстро обрабатывать данные.

Если этот материал Вам немного интересен, то попробуйте
исполнить следующее упражнение.

УПРАЖНЕНИЕ-8. 3

напишите программу для отыскания среднего
арифметического результатов модельного экспе-
римента по бросанию пары игральных костей, сначала попробуйте
предсказать результат чисто теоретически, а потом посмотрите,
насколько совпадает теоретическое предсказание с результатом
вычислительного эксперимента.

Теперь попробуйте сделать все то же самое, но для случая
бросания трех или четырех костей.

8. 3 диапазон.

Когда мы обсуждали результаты вычислительного эксперимента
в предыдущей главе, то мы интуитивно использовали понятие "диа-
пазон". Ны сказали, что результаты серии из 30 экспериментов
оказались в диапазоне от 3. 24 до 3. 76. Определение диапазона
сводится к отысканию максимального и минимального значений.

ПРИНЕР-8.3 Разработать алгоритм и написать программу для
отыскания максимального и минимального значений из
последовательности чисел. приведенных в строке DATA в
ПРИНЕРЕ-2. Если Вы чувствуете себя достаточно уверенно, то
рассматривайте этот пример как упражнение и попытайтесь все
сделать сами до того, как ознакомитесь с нашим вариантом
решения.

Решение Ны уже занимались подобной задачей ранее, в VPOKE-4.

когда отыскивали наименьший элемент списка. Ны могли
бы и здесь поступить так же. но для этого потребовалось бы со-
брать все данные в список и дважды его пересортировать. Это
большой объем работы, поэтону здесь мы поишем более короткий
путь, в поисках наименьшего и наибольшего значения непосредст-
венно в тот момент, когда они вводятся чтением из строки data
или вводятся через ihput.

1. Сначала мы создадим две переменные:

го для текущего максимального значения;
b - для текущего минимального значения.

2. Затем ны примем первое число через READ или через ihput
и поместим его и в "ш" и в "Ь". Пока оно одно, оно ведь
является и минимальным и максимальным.

3. После этого мы будем вводить (считывать) остальные
числа и. если какое-то число окажется больше, чем "п>".
то мы его поместим в "ш". а если оно окажется меньше,
чем "ь". то поместим в "ь". если ни то. ни другое, то
мы его просто проигнорируем и перейдем к следуюшену.

Таким образом, в описательной Форме алгоритн будет выгля-
деть так:

1. Стартовый блок.

2. Вводим первое число. Если счетчик равен 1. то заносим
его и в "т" и в "Ь", после чего переходим на п. б. Иначе
идем на п. 3.

3. Если число больше "т", то засылем его в "т" и переходим
на п. 6. Иначе, идеи на п. 4.

4. Если число больше или равно "ь", то переходим на п. 6.
Иначе идем на п. 5.

5. Записываем это число в переменную "Ь".

6. Коней.

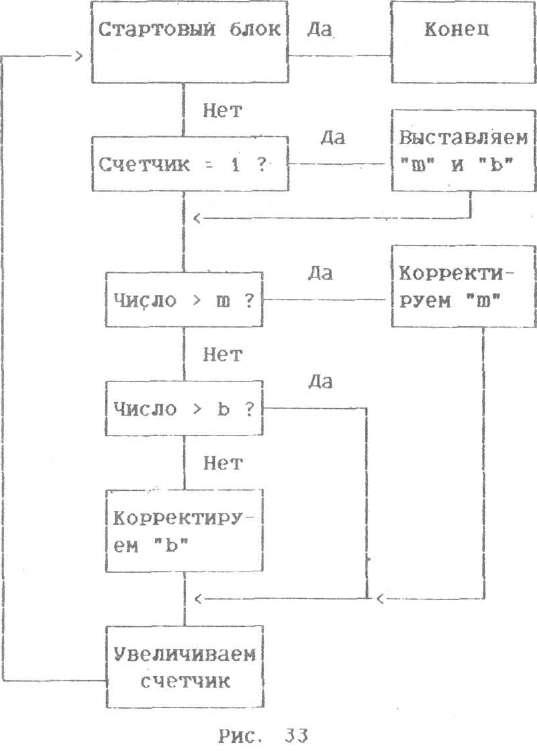
этот же алгоритм в виде блок-схемы выглядит так. как пока-
зано на рис. 33.

Какой алгоритм Вам удобнее, решайте сами. Обычно принято
считать, что если алгоритм линейный и в нем мало ветвлений, то
удобнее описательный алгоритм, а если же в нем иного ветвлений,
то блок-схема лучше. Но решать в итоге все равно ван.

А вот как будет выглядеть этот алгоритм, когда мы воплотин
его в БЕИСИК:

Ю REH »»Нах и Н1П»»

30 REH »»с-счетчик введенных чисел»»

40 LET С-1

50 REM ««s-сумна введенных чисел»»
60 LET s=0

70 REH »«Ввод следующего числа»»
60 IHPUT "Введите число ";ш
90 PRIHT m
100 IF Ш---9999 THEH GO TO 260
110 IF c>1 THEH GO TO 160
130 LET b=m

140 LET t=ffl

160 REH *«Главный цикл»*

1T0 IF m>t THEH GO TO 210

180 IF Ш>=Ь THEH GO TO 230

185 REH ««Новое минимальное число»»

190 LET b=rn

200 GO TO 230

210 REH »«Новое максимальное число»»
215 LET t=m

230 REM »»11рирашение счетчика»»
240 LET c-c*l
250 LET S=S+m
260 GO TO TO

280 REH »«Вывод результатов»»
290 CLS

300 PRIHT "max = t. "Min = ";b
320 LET n=c-l
330 PRIHT

340 PRIHT "Среднее = ";s/n
350 STOP

II - 6613

Тот же самый алгоритм, но переделанный под ввод данных с
помошью read. . . data:

10 REH »«Hax and нт»«

20 LET c-l
30 LET S=0
35 READ m

40 IF m= -9999 THEH GO TO 165

50 IF С >1 THEH GO TO 100

60 REH «*««»**««»««*•*«»«»«««»»»

65 REH ««Ввод первоначальных значений*«

то LET b=m

80 LET t=m

90 REH ««ж*»»»»»»»»»»»»»»»»»»»»»
loo REH ««Проверка на max/mm»»
105 IF m>t THEH GO TO 140
110 IF m>=b THEH GO TO 160
115 REH ««Новое минимальное значение«•
120 LET b=m
130 GO TO 160

140 REH ««Новое максимальное значение»«
145 LET t^ro

150 REH ««e»»»»»»»»»»»»»»»»»»»»»»
160 REH »«Сумма»«

165 LET C=C+1
170 LET s-s+ю
175 GO TO 30

180 REH «.«»««»»»»»»»»»«»»»»»»*«»
185 REH ««ВЫВОД»»
198 PRIHT "Hax = ";t. "Hin = ";b
200 REH к»»»»»»»»»»»»»»»»»»»»»»»

210 LET П= С - 1
220 PRIHT

225 PRIHT "Среднее = ";s/n
230 STOP

240 REH ««i»»»»»*»»»»»»»»»»»»»»»*
250 REH ««Данные»»

900 DATA 56,47,52,65.24,34.59,37,49,66
910 DATA 38.24.62.76,31,47.66.61,74,45
920 DATA 66.44.55.67,36.56.54.54.50,43
930 DATA 18.83.23.79,29.-9999

8. 4 Работа с числани.

До сих пор нам удавалось как-то избегать действий более
сложных, чем элементарная арифметика. Попробуем и дальше дейс-
твовать в том же духе, но было бы все же резонно дать читателю
прдставление о вычислительных возможностях его компьютера. Если
Ваша душа не лежит к такому применению "Спектрума", то можете
несколько страниц снело пропустить, жизненно важной информации
№ при этом не потеряете, но будет все же лучше, если бы их
прочитаете и хотя бы сделаете "сухой прогон", (Так называют
просмотр програни без компьютера. Это как бы запуск программы в
уме).

Перед Вани программа, которая рассчитает квадраты чисел от
1 до ю. их кубы и обратные величины, а затем распечатет ре-
зультат в табулированном виде.

1 КЕН ««Расчет квадратов.

г кец кубов и обратных величин

3 КЕН для первых десяти

4 REH натуральных чисел»»

5 PRIHT TAB 3; "Натенатические таблицы"

6 priht "к**»*»»»»**»»»»»»*»*»***»»*»»»»»*"

в priht

ю priht "n"; tab 5;"n«n";tab 12: "п«п«п";тав 22;"l/n"

20 priht

25 REH ««Вычислительный цикл»»

30 FOR f=l TO 10

35 REH ««число**

40 LET n=f

45 REH ««квадрат**

50 LET S=f«f

55 REH *«КУ6««

60 LET C=f«f«f

65 REH *«обратная величина**
70 LET r=l/f
75 REH ««печать»»

во priht n; tab 5; s: tab 12;c:tab 22; г
90 НЕХТ f

too stop

RUH

Натенатические таблицы

n	n«n	n«n*n	l/n
1	1	1	1
2	4	8	0. 5
3	9	27	0. 33333333
4	16	64	0. 25
5	25	125	0. 2
6	36	216	0. 16666667
7	49	343	0. 14285714
8	64	512	0. 125
9	81	729	0. 11111111
10	100	1000	0. 1
T*

Последовательности » их суммы.

Расчет индивидуальных членов последовательности и суммы
всей последовательности - это очень трудоемкая задача, если у
Вас нет компьютера, прикиньте сами, сколько вренени у вас
займет расчет членов такой последовательности:

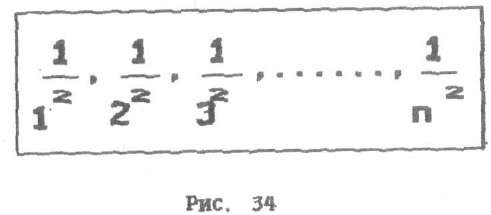
А на компьютере это очень просто:
ю PRIHT "Расчет последовательности"
20 PRIHT

30 PRIHT "П". "n*<-2>"

40 REH ««начало главного шпсла»»

50 FOR П=1 TO 10

60 PRIHT П.П^А(-2)

70 НЕХТ П

80 STOP

RUH

Расчет последовательности

п	ПМ-2)
1	1
г	0. 25
3	0. 11111111
4	. 0625
5	. 04
6	,027777778
7	.020408163
8	.015625
9	. 012345679
10	. 01

УПРАХНЕНИЕ-8. 4

определите, сколько членов последовательнос-
ти надо просуммировать, чтобы их сумма превы-
сила г. 4? Последовательность: 1. 1/г. 1/3, 1/4, 1/5,...

УПРАЖНЕНИЕ-8, 5 измените программу упражнения 8. 4 так. чтобы
-она работала с последовательностью, приведен-
ной на рис. 34

Без Факториалов не обходится ни один учебник
по программированию. Факториал обозначается
знаком "I" Так. например. 4! = 4»3»2»1, а

п! = n«(n-l)»(n-2) «(n-3)«... «1

Напишите программу, которая рассчитает Факториал любого
заданного целого положительного числа.

УПРАЖНЕНИЕ-8. 6

УПРЛЖНЕНИЕ-8. 7 В первом уроке мы рассчитывали сложные процен-
ты по депозитному вкладу, когда процент по де-
позиту со счета не снимается, а остается на вкладе и в дальней-
шем начисляются проценты на проценты. Получившаяся там програм-
ма на самом деле не очень изяшна. Существует более элегантный
подход:

y=d«(l+p/100)"t

у - доход

р - процент по депозиту (годовой)

t - срок хранения денег на счету (лет)

Напишите программу для расчета дохода на заданный депозит
за разные сроки, используя эту Формулу.

8. 5 "сухой прогон".

Очень часто мы обнаруживаем, что написанная нами программа
либо вообше не работает, либо работает не так. как надо. Если
перед вами компьютер, мы можем сидеть за клавиатурой столько,
сколько, хочется, пока не найдем ошибку, но когда все попытки
отладить программу ни к чему не приводят, нам приходится брать
в руки карандаш, распечатку программы и напряженно думать. Про-
ход по распечатке от строки к строке, от оператора к оператору
с помошью карандаша и называют "сухим прогоном".

Ны рассмотрим методику "сухого прогона" на принере про-
граммы. .которая является решением упржнения-8. 4.

10 REH ««Сумма членов последовательности»»
20 PRIHT "Сколько членов последовательности

надо взять, чтобы сумма превысила 2. 4?"

30 LET s=0
35 LET П-i

40 REH ««начало цикла«»
50 LET s=s+l/n
60 IF s>2. 4 THEH GO TO 90
70 LET 11=11+1
80 GO TO 40

90 REH ««вывод на печать»»

100 PRIHT

HO PRIHT "Сумма = s:" количество членов = ";n

120 STOP

Трассировка - это проход по программе не в том порядке, в
котором она написана, а в том порядке, в котором она исполняет-
ся. при этом записываются номера исполняемых строк и значения
переменных, которые они принимают при исполнении данной строки
так. для вышеприведенной программы мы получим следующую табли-
цу.

шаг	Н СТРОКИ	п	s
1
2
и т. д.

НЫ опускаем строки с операторами, которые не влияют на
значения переменных:

rem (строка 10)
go то (строка 80)
priht (строка 100)

Если их исключить, то получим следующий результат (обрати-
те внимание на эффект go то):

step по.	line по.	п	s
1	30	0	0
2	35	1	0
3	50	1	1
4	60	1	1
5	70	2	1
б	50	2	1. 5
7	60	2	1. 5

8	70	3	1. 5
9	50	3	1. 83
10	60	3	1. 83
1 1	70	4	1. 83
12	50	4	2. 08
13	60	4	2. 08
14	70	5	2. 08
15	50	5	2. 28
16	60	5	2. 28
17	70	6	2. 28
18	50	6	2. 45

Трассировка.

Некоторые версии БЕИСИКа имеют команду TRACE, по которой
компьютер сан проделает рутинную работу, которую Вы только что
видели. "Спектрун" такой конанды не инеет. но это не большая
потеря. Обычно по конанде TRACE програннист получает такую гору
инфорнапии. с которой разобраться еше труднее, чен с саной про-
гранной. Это тот случай, о которой говорят, что "за деревьяни
не видно леса". Наилучшим приемон всегда будет составление соб-
ственной трассирующей программы. Если она тщательно продумана,
то дает быстрый эффект. Чуть позже в этом уроке мы остановимся
на этом вопросе поподробнее.

Выполните "сухой прогон" следующей програнны. начиная
со строки 20 и продолжая до того нонента. когда выра-
жение в строке 60 станет справедливый, сделайте таблицу по прй-
веденнону выше образцу.

10 REM ««сунна квадратов»*
20 LET s=0
30 LET П⁼ 1

40 REH **Прибавин очередной член**
50 LET s=s+n*2
60 IF s>50 THEH GO TO 90
70 LET П=П+1

BCK-8. 2

80 GO ТО 40

90 бен ««Вывод на печать»*
100 priht "Сумма квадратов"
110 PRIHT

120 PRIHT "Сунна = ";s;" количество членов - ";п
130 STOP

8. 6 Представление чисел.

До сих пор мы оставляли в стороне вопрос о том. как пред-
ставляются числа в наших программа. Нам не нужно знать о том,
как вообше представляются числа в компьютерах, но не помешает
немного осветить этот вопрос для себя.

В обшем случае компьютеры могут обрабатывать и хранить в
памяти следующие типы чисел:

а) положительные и отрицательные целые числа:

б) дробные числа и составные числа, имеющие целую часть и
дробную часть;

в) очень большие и очень малые числа;

г) число О.

Самый важный совет, какой мы можем дать на этой стадии,
звучит так: "Как только какое-то число оказалось вовлеченным в
математические расчеты, к нему надо Относиться с подозрением",
причина для такого заявления состоит в том, что числа в компью-
тере хранятся и обрабатываются в двоичной форме, а не в десяти-
ричной, к которой мы все так привыкли. Вы знаете, что в нашей
обычной десятиричной Форме записи есть свои ограничения. Так,
если вы захотите записать число 1/3, то у Вас получится
0. 33333... ны, конечно, полагаем, что добавив к хвосту этого
числа еше столько троек, сколько угодно, мы всегда сможем до-
стичь той точности, которая нам нужна для решения конкретной
задачи. 'Точно так же и в двоичной системе есть числа, которые
просто нвозможно выразить точно. Например, в десятиричной сис-
теме число 1/Ю может быть вражено точно о. 1, а в двоичной
системе и это число нельзя выразить конечным числом цифр.

Большая часть БЕИСИК-интерпретаторов позволяет выражать
числа с точностью до шести десятичных знаков. Так. число з+1/Ю
может быть представлено как 3. 10000. Но если это число было
получено в результате каких-то расчетов, Вы легко можете обна-
ружить, что оно равно 3.099999 или 3.100001, т.е. Вы всегда
должны с подозрением относиться к последней цифре в записи чис-
ла.

Програмна 8. 3 показывает, как может возникать этот тип не-
точностей. В иикле FOR. . . НЕХТ к значениям переменных s,t,и при-
бавляются числа 4.0, 4. 1, 4. 25 и так тысячу раз. Теперь подска-
жен, что числа 4. О и 4. 25 имеют точное выражение в двоичной
системе, а число 4. 1 - нет. так что вы поймете, почему в ре-
зультате такого большого количества сложений 4.0 и 4. 25 дали
точный результат, а 4. 1 - имеет небольшую ошибку.

10 КЕМ *«Демонстрация точности*»

20 LET 3=0

30 LET t=0

40 LET U=0

50 FOR f=l TO 1000

60 LET 3=3+4.0

70 LET t = t+4. 1

80 LET U=U+4. 25

90 HEXT f

loo priht s;tab 8; t;tab 2i;u

110 STOP
RUH

4000 4100. 0002 4250

Очевидно, нам следует избегать такого многократного повто-
рения операций с неточными числам везде, где это возможно и. с
этой точки зрения, подобная программа является неграмотной, но
ны ее привели только для демонстрации самой идеи и не более

того.

очень малые и очень большие числа.

Предел точности микрокомпьютеров - от 6 до 10 значащих
цифр и это не позволяет нам иметь дело ни с очень малыми, ни с
очень большими числами, поэтому на БЕИСИКе их выражают в экспо-
ненциальной Форме (ее еше называют нормализованным видом).

Малые числа:

0.000586321 - это то же самое, что и
586321/юоооооооо и то же самое, что и
586321/10*9. это же число можно записать и как
586321»10*-9
Ны можем выразить 0,000586321 и по-другому:

0,000586321 = О.586321«10*-3
На БЕИСИКе такое число запишется, как

О, 586321Е-3
Аналогично:

0,234539 = 2. 34539» 10*-2 = 2.34539 Е-2

и

О. 00000000959734 = О. 959734 Е-8

Буква "Е" произошла от слова "экспонента" (exponent). Ос-
нование экспоненты всегда (в компьютере) равно 10. поэтому по-
казатель Е-4 передвинет десятичную точку на четыре десятичных
знака влево, а показатель Е+9 - на девять десятичных знаков
вправо.

Большие числа.

12366500 = 1. 23685*10*7 = 1.23665 К+2

935.432 = О. 935432» 10*3 = 0.935432 Е+3

959734000000000000000=0. 959734 Е*21

Большая часть интерпретаторов БЕИСИКа позволяет работать с
показателями от Е-32 до Е+32.

10 КЕН »«Демонстрация»«
20 PRIHT "Число, Представление*
зо FOR m=-io то ю

40 PRIHT "I0*";m, 10*ш
50 HEXT m

RUH

число Представление

10*-10 9.9999999E-11

10"-9 l.E-9

10*-8 l.E-8

10^Л-7 l.E-7

10*-6 l.E-6

10* -5 0.00001

10*-4 0.0001

10*-3 0.001

10*-2 0.01

10*-1 0. 1

10*0 1

10*1 10

10*2 100

10*3 1000

10*4 10000

10*5 100000

10*6 1000000

10*7 10000000

10*8 1E+8

10*9 1E+9

10*10 1E*10

8. 7 Применение фнукции IHT для округления чисел.

Во многих случаях нам бывает нужно округлить результат
вычислении до ближайшего целого числа, так, например,

6. 6 до 7

7. 4 до 7.

Это особенно важно, если мы не уверены в точности резуль-

тата и сомневаемся в истинности последнего знака<
6. 99999 или 7. 00001 ДО 7

С помошью функции IHT этого сделать нельзя . поскольку IHT
всегда округляет вниз (мы об этом уже говорили). Но это можно
сделать с помощью функции 1НТ(х+о. 5). вы можете убедиться в
этой на примере следующей программы:
10 КЕН ■«округление чисел*«

20 PRIHT -Х";ТАВ 10! "1НТ(Х)". ТАВ 20; "1НТ(х+0. 5)»

30 FOR f = 1. 4 ТО -2. 5 STEP -О. 1

40 PRIHT f; TAB 10; IHT f: TAB 20: IHT (f+0. 5>

50 HEXT f

60 STOP

X IHT(X) IHT(X+0. 5)

-1.4 -2 -1

-1.5 -2 -1

-1.6 -2 -2

-1.7 -2 -2

-1.8 -2 -2

-1.9 -2 -2

-2 -2 -2

-2. 1 -3 -2

-2. 2 -3 -2

-2. 3 -3 -2

-2. 4 -3 -2

-2. 5 -3 -2

-2.6 -3 -3

Изменив строку 30 на:

30 FOR f = 1. 4 TO 2. 6 STEP . 1
мы получим:

X IHT(X) IHT(X+0. 5)

1. 4 1 I

1. 5 1 2

I. 6 1 2

1. 7 1 2

1. 8 1 2

1. 9 1 2
2 2 2

2. 1 2 2
2. 2 2 2
2. 3 2 2
2. 4 2 2
2. 5 2 2
2. 6 2 3

ВСК-8.3 Попробуйте определить.

рассмотренная программа
следующим образом :

а) 30 FOR f=. 4 TO 2. 2 STEP .2

б) 30 FOR f=. 4 TO 6 STEP -.2

8. 8 Функция ABS

Эта Функция отыскивает модуль (абсолютную величину) числа.
Ее работа очень проста:

ABS (23) = 23
ABS (-23) = 23

Работу этой Функции иллюстрирует следующая программа:
10 rem ««Функция abs««
20 priht "Работа функции abs"
30 priht

40 PRIHT "х"; TAB 7;-У"; TAB 14; "x+y"; TAB 21;"ABS(x+y)•
50 REM ««начало цикла««
60 FOR f=l TO 4
70 IHPUT X
80 IHPUT у

90 PRIHT XiTAB 7; y; TAB 14; X+y; TAB 21; ABS (Х+У)
100 HEXT f

RUH

Работа функции abs

x	у	х+у	abs(х+у)
5	7	12	12
5	-7	-2	2
-5	7	2	2
-5	-7	-12	12

Каковы будут Результаты работы этой программы, если
мы введем через IHPUT следующие числа:
9. 14, 11,-2. -4. 13. -7, -8»

8. 9 Итерации

Процесс, в котором мы угадываем некоторое число, проверяем
его, по результатам проверки делем более точное предположение,
снова его проверяем и т. д. называется итерационным процессом.
Каждый шаг в этом процессе - итерация.

Давайте рассмотрим, как с помошью одного из итерационных
методов можно отыскать квадратный корень из числа п. Суть мето-
да состоит в следующих действиях:

- пробуем угадать результат - в

- рассчитываем величину п/в

- берем среднее значение между в и п/в;

- возвращаемся назад и повторяем наши действия.

Здесь, в принципе, ножет возникнуть вопрос о том, правда
ли. что среднее между "В" и "п/в" это более точное приближение,
чем исходное значение "в"? Ны не будем восходить до изложения
теории численных методов, но скажем только, что это можно дока-
зать теоретически и если Вас интресует такое доказательство, то
Ван надо обращаться к специальной литературе.

Итак, пусть нан надо найти квадратный корень из числа 1г.

Первая итерация.
Число

Предположение

Расчёт

Среднее

Вторая итерация.
Предположение
Расчет
Среднее

и т. д.

век-8. 5 Убедитесь в тон. что Вы хорошо поняли суть предлага-
емого метода. Для этого повторите приведенный расчет,
но в качестве первого приближения возьмите 8=1.

Теперь перед нами встал следующий вопрос: "До каких же пор
надо продолжать итерации? Ответ такой: "Процесс надо продолжать
до тех пор. пока квадрат нашего результата не будет достаточно
близок к числу п". Следующий вопрос: "А что мы подразумеваем
под словами "достаточно близок"?" ответ такой: "Что хотите,
это Ваше дело. Вы хозяин, Вам и решать. " Если №. например, хо-
тите получить результат с точностью до двух цифр после десятич-
ной точки, то квадрат Вашего результата не должен отличаться от
исходного значения п более, чем на о. 005. Кстати, нан неважно,
что 8*8 больше п или неньше п. нас интересует только разность
между ними, и вот здесь-то нам и пригодится Функция АВ5.

если ABS(n-g»8) <о. 005. тогда STOP.
Вот как выглядит алгоритм в описательной Форме:

1. Начало работы.

2. Ввод исходного числа.

3. Ввод требуемой точности.

4. Ввод первого предположения.

.5. проверка, не является ли данное предположение доста-
точно точным для нас решением и тогда переход на п. в

6. Расчет более точного, предположения.

7. Возврат на п. 5

8. Печать результата.

9. Конец работы.

Блок-схена.

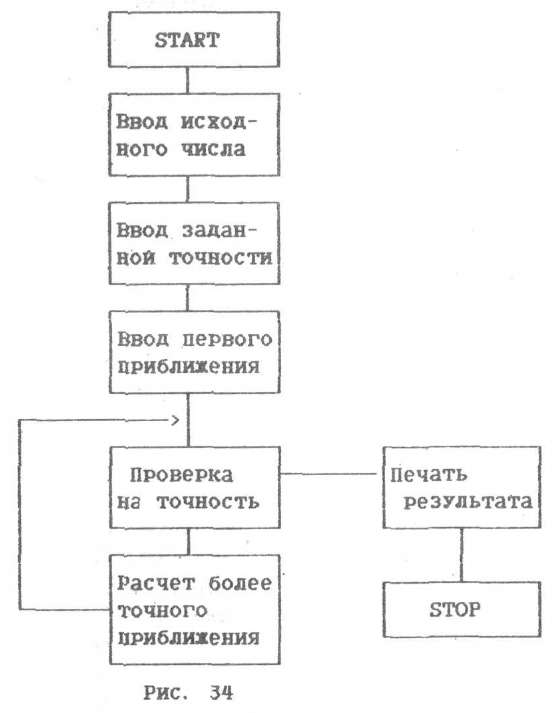
Программа на БЕИСИКе для реализации этого метода будет
такой:

го IHPUT "Исходное число?"; п
30 PRIHT "Поиск квадратного корня из"
40 PRIHT п

50 IHPUT "Введите точность?"; а
60 PRIHT "Требуемая точность ";а
70 INPUT "Первое приближение?"; g
80 PRINT "Вы предполагаете ";g
90 REM »«Начало итераций»»
100 IF ABS(n-g«g)<a THEN GO TO 130
110 LET g = 5«(g + (П/g))

120 GO ТО 90

130 reh ««вывод на печать*»
140 priht

150 PRIHT "Корень квадратный из ";п
160 PRIHT "равен ";в
170 STOP

ruh

Поиск квадратного корня из
12

Требуемая точность . 005
Вы предполагаете 2

Корень квадратный из 12
Равен 3. 4642857

ruh

Поиск квадратного корня из
12

Требуемая точность . 0005
Вы предполагаете 2

Корень квадратный из 12
равен 3.4641016

Использование отладочной печати.

Результат, который мы получили в предыдущей программе осо-
бо впечатляющим не назовешь. Действительно, мы ухе говорили о
том, что для отыскания квадратного корня из числа "Спектрун"
уке имеет соответствующую команду и все можно было бы сделать
гораздо проще. Тем не ненее. нан был нужен какой-то пример для
того, чтобы показать, как работает итерационный процесс, а те-
перь мы посмотрин на это поподробнее. Давайте вставин отладоч-
ные операторы в предыдущую програнну.

85 PRINT

86 PRIHT "БЫЛО"; TAB ю; "Стало";TAB 20; "ABS(n-g«g>"
105 PRIHT g;

115 PRIHT TAB 10; g; TAB 20; ABS (n-g»g)

На каждой проходе (на каждой итерации) в строках 105 и 115
будет распечатываться инФорнапия. по которой ножно будет судить
о ходе итерационнного процесса.

RUH

Поиск квадратного корня из

12

Требуеная точность . 005

Вы предполагаете 2

Корень квадратный из 12
равен 3. 4642857

RUN

Поиск квадратного корня из
12

Требуемая точность . 0005
Вы предполагаете 2

ABS (П-g »8)
4

О. 2499999
О. 0012755059
2. 6077032 Е-8

Примечание "ИНФОРКОНа"

Обратите внимание на то, что для того, чтобы повысить
точность расчета в 10 раз, нам потребовался всего лишь один
дополнительный шаг итерации. Это означает, что принятый нами
метод является не просто "сходящимся", а "быстро сходящимся".
Быстрая сходимость численного метода позволяет значительно со-
кращать время вычислений, а это очень важно для современных
задач, которые требуют многих миллиардов арифметических опера-
ций. из этого примера Вы можете видеть, над чем работают мате-
матики, занимающиеся численными методами матенатической Физики.
Их основная забота - совершенствование известных методов и раз-
работка новых с целью повышения скорости сходимости.

Несколько лет назад, когда машинное время стоило колос-
сальных денег, эта работа имела большое экономическое значение.
Сейчас экономический аспект отошел на второй план, малинное
время не является дефицитом, компьютеров установлено Уже доста-
точно, но, тен не менее, свою важность эта работа не потеряла.
Дело в тон, что создание новых методов, работающих с более вы-
сокой скоростью, позволяет переходить к моделированию на ком-
пьютерах новых задач, решение которых еше вчера казалось немыс-
лимым из-за большой длительности вычислений.

УПРАЖНЕНИЕ-8. 8

Измените программу для поиска квадратного кор-
ня так. чтобы можно было вычислять кубический
корень из числа, в основу итерационного метода положите следу-
ющую Формулу для вычисления последующего приближения <g') через
предыдущее (g):

	1	п
8'	----	(8 +----)
	2	8«8

ОБЗОР УРОКА

Если Вы- внимательно изучили материалы данного урока, то
должны хорошо понимать следующие вопросы:

- расчет среднего арифметического;

- программный поиск максимальных и минимальных значений;

- "сухой прогон" программы;

- представление чисел в экспоненциальной Форме;

- округление чисел с помошью 1НТ<х+. 5);

- использование функции abs;

- итерационные процессы;

- трассирование програнмы и отладочная печать.

ОТВЕТЫ НА ВОПРОСЫ для САНОКОНТРОЛЯ

Сумма = 8+4+2+6+1+7+6+1+4 = 39.
Всего 9 чисел.

Поэтому арифметическое среднее равно 39/9

а)

номер шага	Номер строки	П	s
1	20	0	0
2	30	1	0
3	50	1	1
4	70	2	1
5	50	2	5
6	70	3	5
7	50	3	14
8	70	4	14
9	50	4	30
10	70	5	30
11	50	5	55
X	INT (X)	IHT	(х + 0.
0. 4	0		0
0. 6	0		1
0. 8	0		1
1	0 (»)		1
1.2	1		1

12 - 6613

1. 4 1 1

1.6 1 2

1.8 1 £

2 2 2

(») Примечание: конечно IHT(l) = 1. но поскольку в нашем

примере число 1 получено расетнын путем, то вследствие накоп-
ленной ошибки получается в результате о.

Ь)

	X		INT (X)			INT (x+0. 5)
	0. 4		0			0
	0. 2		0			0
	0		0			0
	-0. 2		-1			0
	-0. 4		-1			0
	-0. 6		-1			-1
		У		Х + У		ABSIX+У)
)		14		23		23
1		-2		9		9
4		13		9		9
7		-8		-15		15
e		П/8			ie+n/g)/2
l		12			6.	5
6.	5	1. 8			4.	15
4.	15	2. 89			3.	52
3.	52	3. 41			3.	46
И	Т. п.

ОТВЕТЫ К УПРАЖНЕНИЯМ

упражнение-8. 1 ю rem ««средняя длина слова»»
=====——j 20 print "Расчет средней длины"
30 let 3=0
35 let C=1

40 REM «» начало цикла»»
50 INPUT "Введите слово: ";w»
60 PRINT w$

70 IF W$^"zzzz" THEN GO TO 130
80 LET p LEN(w$)
90 LET s s'p
1 00 LET С = C♦1
110 GO TO 40

120 REM ншпшниианши
130 REM ««вывод результатов»«

140 LET n c-1
150 LET Я s/n

160 priht "Средняя длина слова"
165 priht "равна ";а;" символов- "
170 stop

Ю reh * * loo бросаний кости»»
зо priht "Бросаем одну кость юо раз"
40 let 3=0

50 REH »«начало цикла»»
60 FOR f=l ТО 100
70 LET X=IHT(6»RHD ♦ 1)
80 LET S=S+X
90 НЕХТ f

100 REH ««вывод результатов»»
110 PRIHT

120 priht "Средний результат = ";s/ioo
130 stop

Iупражнение-8. з| 10 REH »»ioo бросаний пары костей»»
¹ зо PRIHT "Бросаем две кости юо раз"

40 LET 3=0

50 REH ««начало шасла»*
60 FOR f=l ТО 100
70 LET x=IHT(6«RHD + 1)
75 LET y=IHT(6»RHD + 1)
80 LET s=s+x+y
90 HEXT f

100 REH ««вывод результатов»«
110 PRIHT

120 PRIHT "Средний результат = ";з/100
130 STOP

УПРАЖНЕНИЕ-8. 41 10 reh ««сумна обратных величин»»
^ Ч 20 priht "Сколько членов последовательности

обратных величин надо взять, чтобы
их сумма превысила 2. 4?"

30 let s=0
35 let п=1

40 reh »«начало цикла»«
50 let s = s + 1/i1
60 if s>2. 4 theh go to 90
70 let il = n+1
80 go to 40

90 reh ««вывод результата»»
100 priht

110 print "Сумма = ";s;"

120 PRIHT "Количество членов = ";n

130 stop

10 REH ««сумма квадратов обратных величин»»
20 PRIHT "Сколько членов последовательности
квадратов обратных величин надо
взять, чтобы их сумма превысила
2.4?"

30 LET s=0
35 LET П-1

40 REH ««начало цикла»»
50 LET S=S+(1/П)*(i/n)
60 IF 3>2.4 THEH GO TO 90
70 LET П=П+1
80 GO Тб 40

90 REH ««Вывод результата»»
100 PRIHT

110 PRIHT "Сунма = "iSi"

120 PRIHT "Количество членов = ";n

130 STOP

10 REH ««факториалы»»
20 PRIHT "Расчет Факториала любого
положительного числа"

30 PRIHT

40 PRIHT "Для окончания работы введите
число -9999"

50 PRIHT

60 PRIHT "П", "П!"
70 PRIHT

75 REH ««ввод очередного числа»«
80 IHPUT "Очередной Факториал?"; п
90 IF П= -9999 THEH GO ТО 190
100 LET Р=1

110 REH ««Расчет Факториала»»
120 FOR f=l ТО П
130 LET P=P»f
140 НЕХТ f

150 REH ««конец цикла»«
160 REH ««вывод результата»»
170 PRIHT П. Р

180 GO ТО 75

190 REM ««конец работы»«
200 STOP

10 REM «« Сложные проценты ««
20 PRIHT "Расчет сложных процентов"
30 PRIHT

40 IHPUT "Вклад? "; d

45 PRIHT "Вы вложили ";d; "рублей в банк"
50 IHPUT "Процент?"; р

55 PRIHT "под ";p;" процентов годовых"
60 IHPUT "CPOK?";t
65 PRIHT "на с1>ок ";t;" лет."
70 PRIHT

80 PRIHT "годы". "доход"
90 REH ««начало шасла»»
100 FOR f=l TO t
110 PRIHT f.d«(l*P/100)'f
120 HEXT f

130 REH »»конец шасла»»
140 STOP

УПРАЖНЕНИЕ-8. 81 10 REH ««кубический корень»»
I Ч 20 IHPUT "число?" ;n

30 PRIHT "Исходное число:"
40 PRIHT П

50 ihput "Требуемая точность?"; a
60 priht "Требуемая точность: ";a
70 let e=n/2

80 REH »«первая итерация««
85 LET С-1

90 REH ««начало цикла итераций»»
100 IF ABS (П-8»8"в)<a THEH GO TO 130
110 LET 8 = 0. 5»(8 + П/(g»8))
115 LET C=C+1
120 GO TO 90

130 rem »»вывод результатов»»
140 priht "К-во итераций = ";c
150 priht "Корень кубический из ";n
160 priht "равен ";g
170 stop

1. Введение - цель курса, нужен ли вам компьютер?
2. Урок 1 - что может компьютер?
3. Урок 2 - оператор PRINT.
4. Урок 3 - что такое стринг?
5. Урок 4 - переменные.
6. Урок 5 - длина стринга.
7. Урок 6 - случайные числа.
8. Урок 7 - оператор BORDER.
9. Урок 8 - арифметическое среднее.
10. Урок 9 - сортировка.
11. Реклама - вниманию любителей персонального конпьютера "ZX-SPECTRUM".

  Оставте Ваш отзыв:

  НИК/ИМЯ

  ПОЧТА (шифруется)

  КОД