4. математика машинного программирования.
4.1 ВВЕДЕНИЕ*
В микропроцессоре данные передаются комбинациями из восьми битов,
но такое представление неудобно для работы, и поэтому программисты
обычно используют шестнадцатиричное представление.
А2 ШЕСТНАДЦАТИРИЧНОЕ ПРЕДСТАВЛЕНИЕ.
Принцип представления состоит в описании чисел по основанию 16. В
этой Системе счисления первые 10 знаков записываются цифрами отО до 9
и к ним добавляются 6 знаков, записываемых буквами от А до F. Таблица
показывает соответствие чисел 0-15.

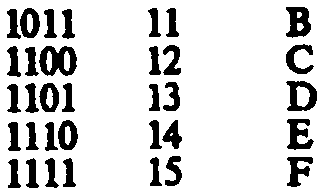
Из таблицы видно, что одна шестнадцатиричная цифра записывается
четырехразрядными двоичными числами, поэтому 8-ми разрядное двоичное
число записывается парой шестнадцатиричных знохов, а для записи 16-ти
разрядного требуется 4 таких знака. Примеры:
00000000 (2-ное) = 00(16)
01001111 (2-hoc)=4F(16)
0000 0000 0000 0000 (2-ное) = 0000/l6)
01001100 1010 1111 (2-ное) =4CAF(16)
Программы 4.1 и 4.2 производят перевод чисел из одной системы
счисления в другую. Первая программа производит перевод из десятичной
системы в любую другую (с основанием от 2 до 16), вторая производит
обратное преобразование. При необходимости перевода числа, например из
восьмиричной системы в шестнадцатиричную, можно сначала
воспользоваться второй программой и перевести восьмиричное число в
десятичное, а затем, используя первую программу, перевести его в
шестнадцатиричное.
10 DIM Ц16)
100 PRINT •CONVERTER OF BASIS'
105 PRINT 'DECIMAL TO (FROM BIN TO HEX)
106 PRINT
107 REM UA3AGE
110 PRINT "DEOMALL-';
120 INPUT Z
125 PRINT Z
130 PRINT 'BASIS ;
135 INPUT В
140 PRINT В
200 LET 1-0
205 LET 14+1
210 LET Rm(Z/B-INT(Z/B))'B
215 LET 1{I)-R
220 LET Z-INT (Z/B)
225 IF Z>-B THEN GO TO 205
230 LET H+l
235 LET L(l)-Z
300 PRINT 'EQUAL *;
305 LET N$-'ABCDEF"
310 FOR >/ TO 1 STEP -1
315 IF L(Jf>- 10 THEN GO TO 350
320 PRINT 1(4;
330 NEXT J
340 STOP
350 LET ЦЛ-Ц4-9
360 PRINT N$(L(Jf);
370 GO TO 330
999 STOP
Программа 4.1 Преобразование десятичных чисел в числа с произвольным
основанием (от 2 до 16) системы счисления.
100 PRINT •CONVERTER OF BASIS
105 PRINT •BIN ■ HEX TO DECIMAL *
106 PRINT
110 INPUT Z$
120 PRINT Z$
130 PRINT •BASIS:■ *
140 INPUT В
150 PRINT В
160 LETN-0
170 LET L- LEN Z$
175 GOSUB 300
180 FOR hi TO L-1
182 LET E-CODE Z$(ll
184 IF E>58 THEN LET E'E-7
190 LET N-(N+ E -48)'B
200 NEXT I
205 LET E-CODE Z$(L)
207 IF E>58 THEN LET E-E-7
210 LET N-N+E -48
220 PRINT ' DECIMAL: 'N
230 STOP
300 FOR /-/ ТО L
305 LET C-CODE Z$(IHS
306 IF 010 THEN LET C-C-7
310 IF C>-B THEN GO TO 350
315 NEXT 1
320 RETURN
350 PRINT mCONVERTING NOTABLE9
999 STOP
Программа 4.2 Программа преобразования чисел с произвольным основанием
(от 2 до 16) системы счисления в десятичные.
Одинарный регистр или ячейка памяти содержит 8-ми битовое двоичное
число. Это число может быть в диапазоне 0000 0000-1111 1111. Ни в одном
из этих случаев число не может быть ни отрицательным, ни дробным, и это
образует основу абсолютной двоичной арифметики: значение в памяти или
в регистре всегда положительное и целое.
Также важно представлять себе, что значение, содержащееся в памяти
или в регистре, изменяется циклически в пределах от 0 до 255. Это означает,
что если в операции сложения полученное значение превышает число 255,
то окончательный результат записывается после вычитания 256, а при
вычитании к значению меньше 0 прибавляется 256.
Это показано на следующих примерах.
Флаг переноса действует в большинстве операций, требующих переноса.
Для дальнейшей детализации смотри Главу 5.
В системах основанных на Z-80 все числа представлены в абсолютной
двоичной арифметике, но программист часто нуждается в различном
представлении чисел, таких как положительное или отрицательное, целое
или дробное.
4*3 АБСОЛЮТНАЯ ДВОИЧНАЯ АРИФМЕТИКА.
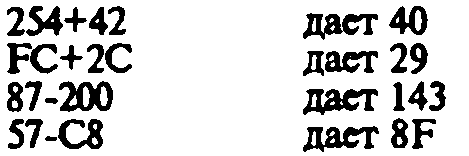
АЛ ДОПОЛНИТЕЛЬНАЯ АРИФМЕТИКА.
Принцип дополнительной арифметики очень прост, но при использовании
ее в программе результат может быть неожиданным для неискушенного
программиста.
Метод позволяет рассматривать программисту,, двоичные значения в
интервале 0000 0000 - 0111 1111, как эквивалент десятичных значений от 0 до
127, а двоичные значения в интервале 1000 0000 -1111 1111, как эквивалент
десятичных значений от -128 до -1.
В результате такой интерпретации бит 7 (левый крайний бит 8-ми
битового числа) рассматривается как знаковый. Он будет 0 для
положительного числа и 1 для отрицательного.
Заметим, что возможно распространить принципы дополнительной
арифметики на 16-битовые числа. В этом случае интервал возможных
значений десятичных чисел будет от -32678 до 32767.
Преобразование отрицательных десятичных чисел в дополнительную
двоичную или 16-ричную форму несложно.
Порядок следующий:
1. Найдите двоичную форму для абсолютного двоичного значения,
например:
-54 = 00110110
2. Получите обратный код (для этого необходимо изменил» 0 на 1 и
наоборот).
00110110=11001001
3. Прибавте 1.
11001001+1=11001010
4. Используйте двоичную форму или переведите в 16-ричную.
-54 в дополнительном коде = 1100 1010 или CAh.
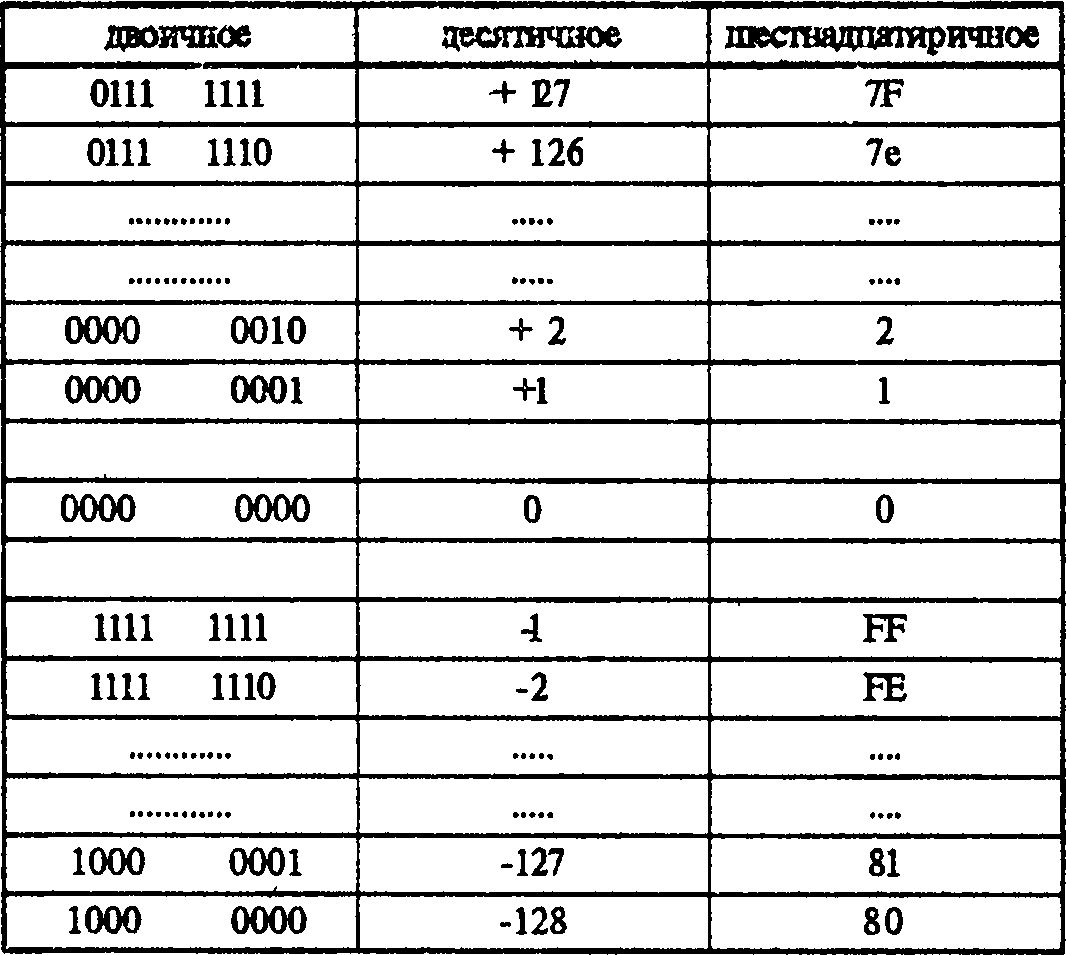
Операцию можно провести в обратном порядке для перевода числа в
дополнительном коде в десятичный вид. Ниже приведена таблица
соответствия двоичного, десятичного и шестнадцатиричного представления
чисел в дополнительном коде.
4.5 ЦЕЛОЧИСЛЕННОЕ ПРЕДСТАВЛЕНИЕ.
Интерпретатор бэйсик в системе SPECTRUM использует 5 байт для
представления чисел. Любое целое в интервале от-65535 до +65535
включительно записывают в целочисленной форме, в то время как любые
дробные или целые числа вне этого диапазона записываются в 5 байт в воде
числа с плавающей точкой.
В целочисленной форме первый байт всегда 0. Второй байт содержит 0,
если число положительное, и 255 (FF), если оно отрицательное. Третий и
четвертый байты содержат целое значение как 16-битовое беззнаковое
число в дополнительном коде. Третий байт содержит всегда младшую часть,
а четвертый - старшую. Пятый байт не используется, но всегда содержит 0.
Следующая программа демонстрирует целочисленную форму (в
десятичном виде) для любых целых чисел вводимых, пользователем. Строка
20 программы гарантирует получение целочисленной формы.
10 INPUT N
20 IF No/NT N OR N<-65535 OR N>65535 THEN GO TO 10
30 PRINT *NUMBER CHOSEN ~:N
40 LET V-PEEK 23627+256*PEEK 23628
5QFORA-1 TO 5
60 PRINT А; Г JAB 5;PEEK(A+V)
70 NEXT A
80 GO TO 10
Программа 4.3
В приведенной выше программе указатель указывает на начало поля
переменных и адреса с +1 по +5 будут содержать 5 байт введенного числа.
Программа дает результаты в виде:
Выбрано значение 0
1.0
2.0
3.0
4.0
5.0
так как 0 положителен и представляется как 0*1+0*256.
Выбрано значение 1516
1.0
2.0
3.236
4.5
5.0
так как 1516 положительно и представляется как 236*1+5*256.
Выбрано значение -1.
1.0
1255
3.255
4.255
5.0
так как -1 отрицательно и имеет форму FFFF.
Замечание : ошибкой программиста будет перевод -65536. Это значение
не соответствует целочисленной форме 0, 255, 0, 0, 0.
4.6 ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ ТОЧКОЙ.
Пять байт, используемых в системе SPECTRUM для представления
чисел с плавающей точкой, позволяют хранить числа в диапазоне 0.29е-38
- 1.7е38 (приблизительно).
Нулевое значение всегда хранится как 5 нулевых байтов. Все остальные
значения хранятся: экспонента - в первом байте, мантисса в остальных
четырех. Теория описания чисел в терминах экспонент и мантисс
первоначально появилась в десятичной записи, поскольку в ней лучше
работать.
Нахождение экспоненты и мантиссы десятичного числа - это в сущности
перевод числа в е-формат. Рассмотрим число 1234, которое в е-формате
может быть представлено как точка 1234 е+4. Для получения мантиссы
десятичная точка двигается влево до тех пор, пока она не становится перед
значащей старшей цифрой. Экспонента - число необходимых сдвигов,
мантисса -дробное десятичное число. Экспонента = +4; мантисса = 0.1234.
Поскольку система SPECTRUM имеет дело скорее с двоичными числами,
чем с десятичными, подобные операции могут быть рассмотрены для
двоичного числа.
Рассмотрим двоичное число 0001 1111, что эквивалентно +31. Двоичная
точка лежит справа от 8-го бита и требует +5 сдвигов, чтобы перевести ее
перед старшим значащим битом. Поэтому экспонента = +5: мантисса=
.11111000.....
В SPECTRUMe производятся еще некоторые действия. Для экспоненты:
экспонента всегда увеличивается на десятичное значение +128 (16-ное 80),
в нашем примере +5+128 = 133.
Для мантиссы: первый бит мантиссы всегда будет единичным, поэтому
его можно использовать как знаковый: для положительного числа он будет
0, а для отрицательного останется 1.
В нашем примере мантисса становится .0111 1000 ... И теперь остается
поместить число в 5 байтов. Неиспользуемые байты мантиссы зануляются.
В десятичном плавающем виде +31 записывается как 133,120,0,0,0 в
шестнадцатиричном 85,78,00,0-0,00 и, если хотите, в двоичном 10000101
01111000 00000000 00000000 00000000.
Подобная операция позволяет переводить и отрицательные и дробные
числа, хотя и не так просто. Следующая программа показывает десятичную
форму чисел с плавающей точкой. Включение строки.30 гарантирует, что
всегда получится форма представления числа с плавающей точкой.
10 INPUT N
20 IF N-0 THEN GOTO 40
30 LET N-N+.2E-38
40 PRINTmNUMBER CHOSESE"fN
50 PRINT
60 PRINT "ЕХРв;ТАВ 0;'MANTISSAm
70 LET V-PEEK 23627+256'PEEK 23628
80 PRINT PEEK (V+1);TAB 0;
90FORA-2 TO 5
100 PRINT PEEK(V+A); CHR$ 32;
110 NEXT A
120 PRINT
130 GO TO 10
Программа 4.4
Приведенная выше программа дает следующие результаты:
Э Kffl, мотгиссэ
1 - 1290000
2 = 1300000
35456 « 1441012800
-1 » 129128000
-35456 = 14413812800
6.333 - 13174167239158
0.5 = 127127255255255
1/2 = 1280000
Можно отметить, что 0.5 и 1/2 дают различный результат.