Андрей Дымура (Кировоград)
ИГРА ГРАНДИ
Успех в использовании ЭВМ
Условия игры
Имеется одна общая группа, содержащая п предметов. Играют двое. Хо-
дят поочередно. Игра начинается с того, что один из соперников разбивает ис-
ходную г|. /ппу на две неравные. Далее, выполняя очередной ход, каждый
соперник разбивает любую из имеющихся групп на две неравные.
Игра продолжается до тех пор, пока все группы не будут состоять из одно-
го или двух предметов. Победитель в игре считается тот, кто сможет выпол-
нить последнее разбиение.
Меня очень заинтересовала возможность построения общего алгоритма
для этой игры. Хочу сообщить, что алгоритм беспроигрышного поведения в
игре Гранди уже найден. Этот алгоритм обладает одной интересной особен-
ностью: он годится для любого заданного числа п, однако для этого же п
должна быть построена специальная вспомогательная таблица. Я попытался
построить таблицу для п = 50. Это оказалось принципиально не сложным, но
довольно трудоемким занятием. Причем с ростом п быстро растет и трудо-
емкость заполнения таблицы. Здесь уже не обойтись без компьютера.
Автором вышеупомянутого алгоритма беспроигрышного поведения в игре
и правил формирования вспомогательной таблицы является мой учитель про-
граммирования, преподаватель Кировоградского высшего летного училища
гражданской авиации Кузнецов С.Т.
Привожу ниже, с разрешения Сергея Тихоновича, идею алгоритма и про-
грамму на БЕЙСИКе для формирования вспомогательной таблицы.
Суть алгоритма
Алгоритмы, задающие беспроигрышную стратегию в играх, должны содер-
жать ответ на два вопроса.
- Каким по очереди вступать в игру?
- Как расчитывать каждый свой ход?
Ответы на оба вопроса для игры Гранди можно всегда получить на основа-
нии информации, содержащейся во вспомогательной таблице. Здесь пред-
ставлена часть таблицы, которой можно пользоваться, если число предметов в
каждой из имеющихся групп не превосходит пятидесяти четырех.
Зная начальное количество предметов п из таблицы, сразу же можно уз-
нать, каким по очереди вступать в игру, и если вступать первым, то какой ход
нужно сделать. На протяжении всей игры, из той же таблицы мы сможем по-
лучать рекомендации относительно каждого своего хода. В итоге мы всегда
одержим победу, выполнив последнее разбиение.
Весь процесс игры можно рассматривать как смену проигрышных и выиг-
рышных позиций для каждого из соперников. Известно, что всякую выигрыш-
ную позицию (для делающего ход) можно всегда перевести в проигрышную
позицию для соперника. Однако свою проигрышную позицию никаким ходом
нельзя перевести в проигрышную для соперника.
Цель первого, как и всех последующих ходов, — создание проигрышной
позиции для соперника.
Для делающего ход признаком проигрышной позиции является равенство
нулю ним-значения. Величина ним-значения выбирается из второго столбца
таблицы.
Ним-значение есть двоичная функция от n (NZ(n)) Если NZ(n) = 0, то пер-
вый ход следует предложить сделать сопернику. Если же NZ(n) = 0, то в игру
следует вступать первым.
Рассмотрим на примере расчет своего первого хода. Пусть п = 48. Соответ-
ствующее NZ(48) = IOO2 = 0. Это значит, что первый ход за нами. Количество
отделяемых предметов находим в нулевом столбце вторых ним-сумм
(NS2 = 0). В нашем примере на пересечении строки п = 48 и столбца NS2 = 0
обнаруживаем число 21 — это и есть отделяемая нами на первом ходе груп-
па предметов.
Рассмотрим пример расчета очередного хода. Пусть в процессе игры об-
разовались шесть групп, содержащих 27,28,35,47,30 и 14 предметов.
Соответствующие им ним-значения находим из таблицы:
NZ(27)= 1002, NZ(47)=1012
NZ(28) = 001 о, NZ(30) = 0112
NZ(35) = 0102f NZ(14) = 0102
В дальнейшем будем использовать понятие первой ним-суммы Первая
ним-сумма есть сумма по модулю два всех ним-значений. В данном случае
имеем:
27 — 100
28 — 001
35 — 010
47 — 101
30—011
14 — 010
011 NS1 = 0112
Полученное значение NS1=0112 позволяет определить, какую из шести
групп разбивать и как это делать.
Вспомогательная таблица
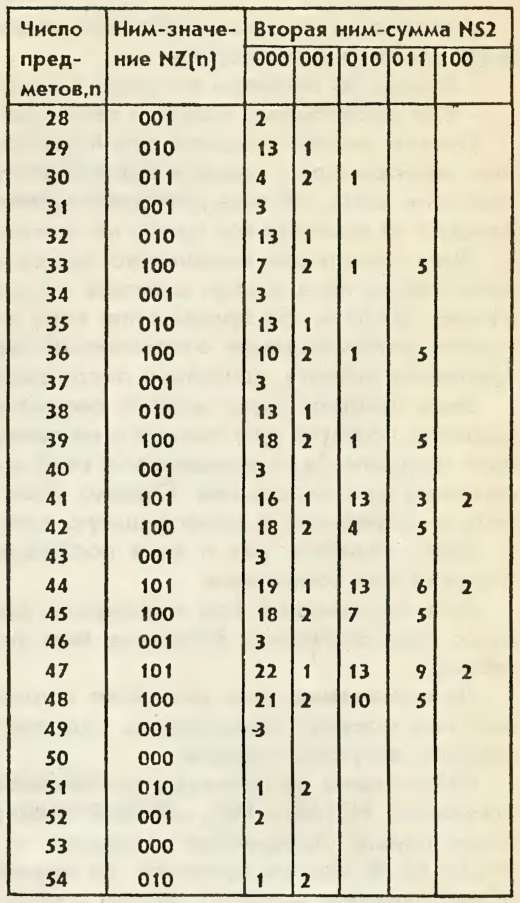
Находим старший разряд в NS1, который содержит "1" — это в нашем
примере второй разряд. Отсюда следует рекомендация: разбиению следует
подвергать ту из групп, в записи ним-значения которой имеется единица во
втором разряде.
В данном случае разбиению можно подвергать любую из трех групп в
35,30 или 14 предметов.
Пусть выбрана группа, содержащая 14 предметов. Для этого находим вто-
рую ним-сумму: NS2 = NS1 + NZ (14). Вторая ним-сумма (NS2), как и первая
(NS1), есть сумма чисел по модулю два. В нашем случае
NS2 = 0012 + 0102 = 0012 • Теперь, зная NS2 = 0012, количество отделяемых
предметов находим на пересечении строки п = 14 и столбца NS2 = 00l2- Там
обнаруживаем число "2". Следовательно, в резальтате нашего хода группа из
14 предметов распадается на две: 2 и 12.
После этого в игре образуется семь групп и соответствующая NS1 = 0002-
Следовательно, как и предполагалось, соперник вынужден делать ход в про-
игрышной для него позиции.
Из сказанного ясно, что главным является формирование вспомогательной
таблицы.
Ниже приводится текст программы, которая генерирует вспомогательную
таблицу для любого наперед заданного натурального п. Естественно, ограни-
чения на п налагаются физическими возможностями конкретного компьютера.
Программа-гонератор вспомогательной таблицы
10 CLS
20 INPUT "Число предметов n"; V%
30 DIM Т% (63),Ke/o(V%)
40 N% = 0
JO N% = H% + 1
60 IF №/o>V% THEN END
70 J% = -1
80 J% = J% + 1
90 IF T%(J%)>0 THEN 80
100 K%(N%) = J%
110 LPRINT "n = ";N%;"NZ = ";BIN$(K%(N%)J;" NS2:";
120 1 = 0
130 IF l% = J% THEN 170
140 LPRINT T%(l%);
150 1% = 1% -I- 1
160 GOTO 130
170 LPRINT
180 FOR 1% = 0 TO 63
190 T%(l%) = 0
200 NEXT 1%
210 M% = INT|N%/2)
220 1% = M%
230 IF 1% = 0 THEN 50
240 S% = K%(l%) XOR K%(N% + 1-1%)
250 T%(S%) = 1%
260 1% = l%-1
270 GOTO 230
После введения пользователем числа предметов программа на принтер
зыводит компоненты таблицы.
Краткость программы позволяет надеяться, что заинтересованный читатель
то ее тексту сможет восстановить для себя алгоритм формирования таблицы.
Отмечу кратко, что мне удалось составить программу-консультант для иг-
эы Гранди, которая для определенных групп предметов, возникших на лю-
5ом этапе игры, либо сообщает выигрышный ход, либо выдает информацию о
проигрышности исходной позиции. Программа работает с готовым фрагмен-
гом вспомогательной таблицы, и поэтому в моем варианте число предметов в
<аждой группе не может быть более ста.
Литература
1. Гарднер М Математические головоломки и развлечения. — М Мир, 1971.
2. Гарднер М. Математические новеллы. — M.: Мир, 1974.
3. Касаткин В.Н., Владыкина Л.И. Алгоритмы и игры. Киев: Рад.шк., 1984
4. Нильсон Н. Искусственный интеллект. — М : Мир, 1973
Комментарий специалиста
Сообщение кировоградского десятиклассника Андрея Дымуры, пришед-
иее недавно в клуб "Терминал", вызывает большой интерес.
Секрет беспроигрышного поведения в игре Гранди непрост. Немало мате-
матиков во всем мире трудились над его поиском.
Предложенный выигрышный алгоритм, безусловно, красив. Но важнее, по-
жалуй, следующее обстоятельство. Существует общеизвестная, хорошо раз-
работанная еще в 1901 году профессором Гарвардского университета Чарль-
зом Л.Бутоном теория игры НИМ. Именно обобщение этой теории привело к
построению алгоритма игры Гранди. Дело в том, что в игре НИМ ним-значе-
ние (NZ(n)) совпадает с двоичной записью числа п, а вторая ним-сумма (NS2),
переведенная в десятичную систему, совпадает с числом предметов, которое
нужно оставить в соответствующей группе. Эти совпадения можно считать
"счастливой случайностью". В других подобных играх дело обстоит не так про-
сто, и тогда, как в игре Гранди, нужно пользоваться вспомогательной табли-
цей.
Я располагаю любопытными примерами игр, которые сообщил мне С.Куз-
нецов. Они порождены изменением правил игр НИМ и Гранди. Игры на пер-
вый взгляд разные. Однако небольшие изменения в программе-генераторе
вспомогательной таблицы позволяют конструировать для этих игр выигрыш-
ные алгоритмы.
Вышеизложенное позволяет говорить не об отдельных играх, а о целом
классе игр, которые условно можно назвать "Ним-игры".