

Ill Всесоюзная олимпиада
по информатике
В Харькове состоялась III Всесоюз-
ная олимпиада по информатике.
Старшеклассники почти из всех ре-
спублик (не была представлена толь-
ко Литва) участвовали в двух турах
олимпиады: теоретическом и практи-
ческом.
Решая задачи первого тура, они
демонстрировали свое умение логи-
чески мыслить, проявлять смекалку и
изобретательность, а также умение
создавать математические модели и
их анализировать. Второй тур — это
экзамен на технику работы за пуль-
том ЭВМ. Школьникам были пред-
оставлены на выбор ПЭВМ "ЯМАХА"
или IBM PC.
Из 87 участников лучшие резуль-
таты у Дмитрия Козлова (Ленинг-
рад), Юрия Зайцева (Украина) и Оле-
га Таборовец (Белоруссия). Диплома-
ми отмечены работы Рейнв Варблане
(Эстония), Алексея Демакова
(РСФСР).
Членам нашего клуба предлагают-
ся две задачи теоретического тура.
Представьте, что вы на олимпиаде и
дерзайте, попробуйте решить задачи
за 6 часов.
1. Круг разрезан по несамопере-
секающейся ломаной с вершинами,
каждая из которых задана парой на-
туральных чисел (Х1,У1,...,Хк,Ук).
Первая и последняя вершины ле-
жат на границе круга, а остальные
внутри его. Определить, можно ли
раздвинуть круг по линии разреза на
две части (выход из плоскости круга
не допускается)?
2. Сколько (Р, Q) коней необходи-
мо для контроля:
а) ограниченной шахматной доски
размером МхК клеток;
б) бесконечной полосы шириной М
клеток;
с) неограниченной плоскости.
Примечание 1: (Р, Q) конь —
шахматная фигура, которая за один
ход перемещается на Р клеток по
горизонтали и Q клеток по вертикали
или на Р клеток по вертикали и Q
клеток по горизонтали. Например, (1,
2) — это обычный шахматный конь.
Примечание 2: Фигура или группа
фигур контролирует поле, если каж-
дая клетка поля доступна за один или
несколько ходов хотя бы одной фи-
гуре. Например, для контроля доски
размером 8x8 необходим один конь
или два слона.
В.Н.Касаткин
Задача Всесоюзной олимпиады по основам информатики 1990 г.
Юрий Волынский
(г.Симферополь, МАН "Искатель")
Краткое описание алгоритма
Рассмотрим круги 1 и 2, изображенные на рисунках. В каждом из них про-
ведены ломаные, разбивающие круги на две части. Требуется определить,
раздвинутся ли части кругов на плоскости.
Для ответа на вопрос будем перебирать все пары звеньев ломаной, иск-
лючая соседние. Перебор осуществляется следующим образом: первое зве-
но (i) рассматривается со всеми последующими звеньями (к), начиная с треть-
его; второе (i) — со всеми последующими (к), начиная с четвертого и т.д.,
при этом звенья (i) назовем базовыми , а звенья (к) — сравниваемыми. Для
каждого звена определим "начало11 и "конец" так, что первая вершина ло-
маной будет началом первого звена; вторая — концом первого и началом
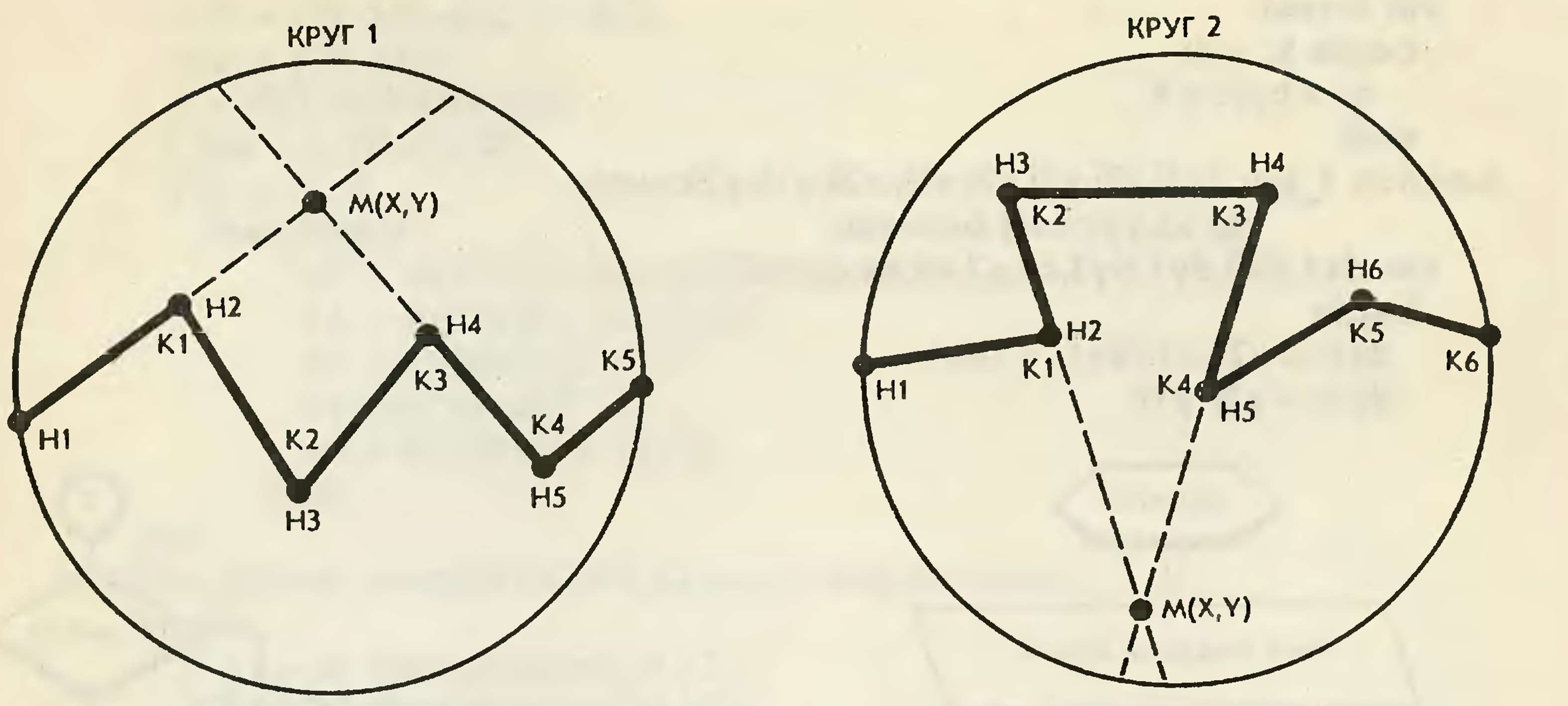
второго; третья — концом второго и началом третьего и т.д. Перебор осу-
ществляется до тех пор, пока не встретится пара, для которой выполняется ни-
жеследующее условие, состоящее из двух частей:
1-я часть — начало i-ro звена ближе к точке пересечения прямых, обра-
зуемых рассматриваемыми звеньями, чем его конец;
2-я часть — конец к-го звена ближе к точке пересечения прямых, образу-
емых рассматриваемыми звеньями, чем его начало. Тогда перебор прекра-
щается и можно сказать, что части круга не раздвинутся. Если такой пары не
встретится, то части круга раздвинутся.
Если точка пересечения прямых принадлежит i-му звену, то достаточно
проверить выполнение только второй части условия, если же она принадлежит
второму звену, то достаточно проверить выполнение только первой части ус-
ловия.
Если два рассматриваемых звена имеют общую точку, то части круга не
раздвинутся. Параллельные звенья не рассматриваются.
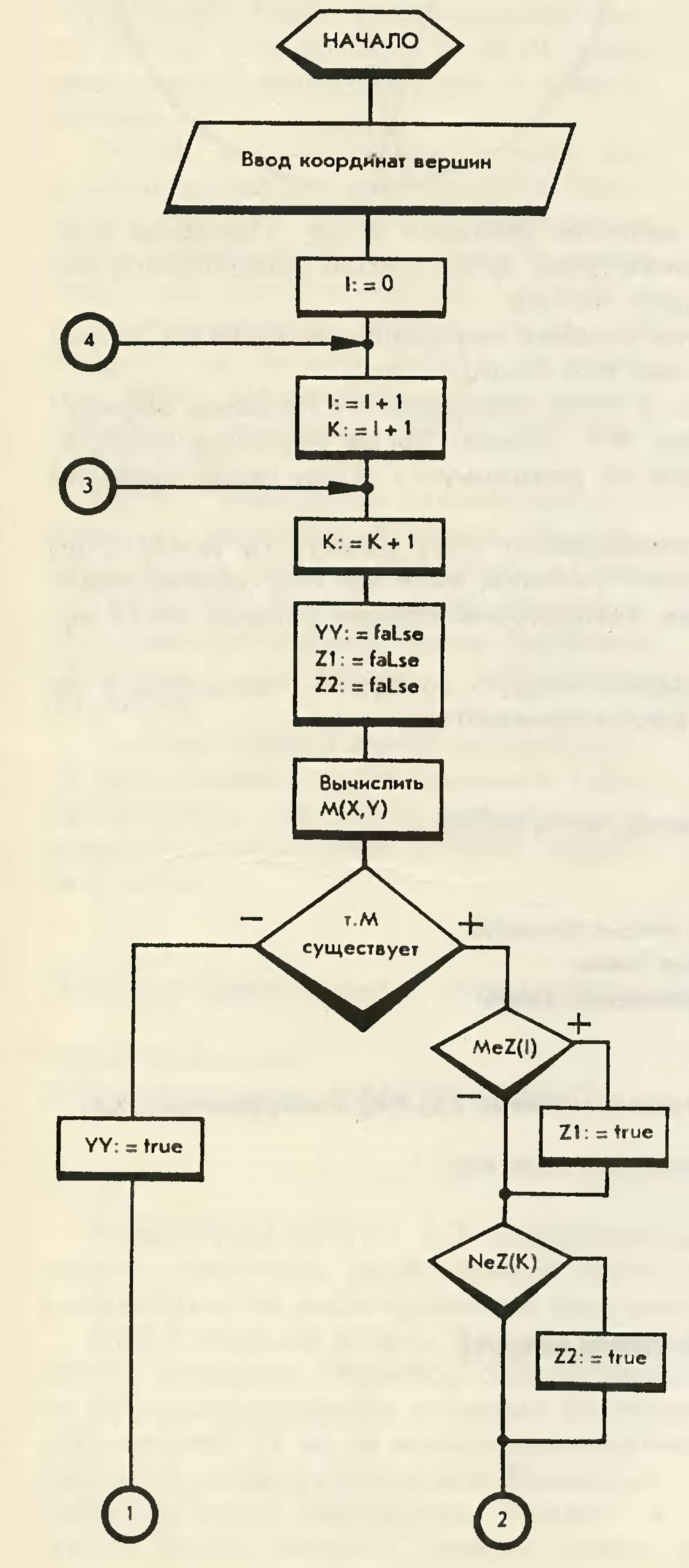
YY,Z1,Z2 — булевы переменные;
YY = {истинна, если полуплоскости раздвигаются, иначе ложна;
N — количество вершин ломаной;
I — обозначает базовые звенья ломанной;
К — обозначает сравниваемые с базовыми звенья ломаной;
N(I),N(I+1) — вершины, образующие базовое звено;
N(K),N(K+ 1) — вершины, образующие сравниваемое звено;
Z(l) — базовое звено;
Ц2) — сравниваемое с базовым звено;
M(X,Y) — точка пересечения прямых, образуемых звеньями Z(I),Z(K), с координатами X,Y;
HI — расстояние от N(1) до M(X,Y);
К1 — расстояние от N{1+ 1J до M(X,V);
N2 — расстояние от N(K) до M(X,Y);
К2 — расстояние от N(K+ 1) до M(X,Y);
PROGRAM {СДВИГ НА ПЛОСКОСТИ} A (input,output);
type massiv = аггау[1..60] of real;
var i,k,kol_ver: integer;
nsn_ysl,z1,z2: boolean;
xm,y m,n 1 rk 1 f n2r k2pf: real;
x,y:massiy;
procedure swapval (arb:real);
в
var krreal;
begin k: = a;
a: = b;b: = к
end;
function t_per (x1i,x2i,y1i,y2i,x1k,x2k,y1k,y2k:real;
var xxryy:real):boolean;
var dx1,dx2,dy1rdy2,c1rc2,dx,dy,d;real;
begin
dxl: = x2i-x1i;dx1: = -dxl;
dy1: = y2i-y1i;
dx2: з x2k-x1k;dx2: = -dx2;
dy2: = y2k-y1k;
d: = dy1*dx2-dy2*dx1;
t per : = (d< >0);
if d < > 0
then begin
cl: = dy1*x1i + dxl'yli;
c2: = dy2#x1k + dx2'y1k;
dx: = c1*dx2-c2*dx1;
dy:dy142-dy241;
xx: = dx/d;yy: = dy/d;
end;
end;
function prinad_zveny(a1,a2Tb1,b2,xx,yy:real):boolean;
begin
if al >a2 then swapval(a1,a2);
if bl >h2 then swapval(M,h2);
prinad_zveny: = ( (xx> = al) and (xx< = a2)
and (yy> = Ы) and (yy< = b2) }
end;
function rasst (x1,x2ry1,y2:real):real;
begin
rasst: = sqr((x2-x1 )*(x2-x1) + (y2-y1)#(y2-y1))
end;
BEGIN
жгйе('Количество вершин ломаной ? ');readln( kol_ver);
if kol_ver > 3 then
Begin
writeln(");
writelnj'BeoA координат вершин.');
for i: = 1 to kol ver do
begin
writeln(' = = = = = = = 'л'-ая вершина = = = = = = =');
writefKoopAHHaTa x? );read(x[il);
write('KoopAHHaia Y? ');read(y[i]j;
end;
writeln;
i: = 0;
repeat i: = i + 1;
k: = i + 1;xm: = 0;ym: = 0;
repeat k: = k + 1;
osn_ysl: = false; zl: = false; z2: = false;
if t_per( x[i],x[i + 1},y[i],y[i + 1];
x[k],x[k + 1],y[k],y[k + 1]rxmrym)
then begin
if prinad_zveny(x[i],x[i + 1],y[i],y[i + 1],xm,ym)
then zl: = true;
if prinad_zveny(x[k],x[k + 1]<y[k],y[k + 1],xm,ym)
then z2: = true;
if not ( zl and z2 )
then begin
if not(zl)
then begin
nl: = rasst(xm,x[i],ym,y[i];
kl: = rasst(xm,x[i + t],ym,y[i + 1]);
if not ( nl <k1 ) then osn_ysl: = true;
end;
if not(z2)
then begin
n2: = rasst([mrx[k],ym,y[k];
k2: = rasst jxmx[k + 1]fymry[k + 1]);
if not (k2<n2 ) then osn_ysl: = true;
end;
end;
end
else osn_ysl: = true;
until ( (k> = kol_ver-1) or not (osn_ysl) );
until ( (i> = kol_ver-3) or not (osn_ysl) );
if osn_ysl
then writeln('PA3flBHrAETCfl')
else writeln(/HE РАЗДВИГАЕТСЯ');
End
else уугйеЦ'РАЗДВИГАЕТСЯ );
readln(f);
END.