ВЕКТОРНАЯ ГРАФИКА
Сегодня мы предлагаем Вашему вниманию небольшой отрывок из главы готовящейся сейчас книги "Прикладная графика". Книга является логическим продолжением ранее вышедшего тома "Элементарная графика", а глава, отрывок из которой здесь приведен, посвящена одной из проблем трехмерной векторной графики.
Вам, конечно, неоднократно приходилось сталкиваться с векторной графикой в игровых программах. Практически полностью на ней построена любимая игра тысяч наших читателей "ELITE", та же графика в программах "ACADEMY', "STARION" и в очень необычной, увлекательной программе, требующей тонкого расчета и стратегического мышления -"CENTINELL". Список игр, инкорпорирующих векторную графику, мог бы быть очень и очень обширным и среди них многие относятся к лучшим из лучших.
Вы, уважаемые читатели, обратили, конечно, внимание на то, что векторная графика в этих играх одноцветная, угловатая и художественными достоинствами очевидно не отличается. Так почему же они пользуются таким успехом, с чем он связан?
Да, конечно, векторная графика выглядит на экране победнее, чем многоцветная растровая графика, но у нее есть два огромных преимущества.
Во-первых, это очень быстрая графика. Цикл освежения экрана и перестроения изображения происходит намного быстрее, чем в программах с растровой графикой.
Во-вторых, это вычисляемая графика, то есть не надо хранить в памяти компьютера заранее подготовленные экраны. Все изображения рассчитываются по заданным алгоритмам и практически никогда не повторяются. Благодаря этому Вы можете иметь в таких программах тысячи планетных систем, десятки возможных кораблей противника и нескончаемое разнообразие игровых ситуаций.
Вспомним программу "ELITE". Да, конечно, нужно иметь воображение, чтобы принять угловатую "морковку" на экране Вашего монитора за роскошный корабль "Fer-de-Lance", нашпигованный чудесами науки и техники и отделанный изнутри лучшими породами дерева и самыми дорогими материалами.
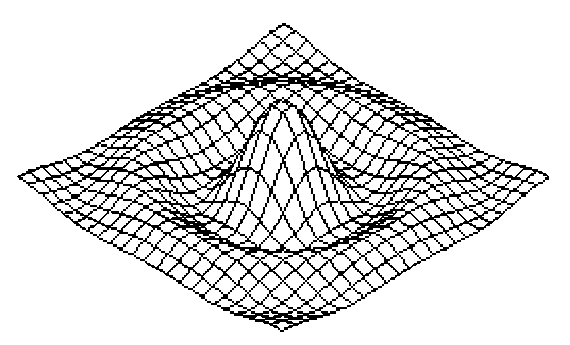
Рис. 1. График функции Z=SIN(R)/R, где R = SQR (X*X + Y*Y)
Параметры приняты такими, как приведенные в БЕЙСИК-распечатке. Другие параметры дадут иную поверхность.
Но зато когда он вращается вокруг всех собственных осей и при этом летит в пространстве, изменяя свои координаты относительно Вашего корабля, а Вы вместе с ним при этом перемещаетесь и маневрируете относительно планеты, звезды, станции и прочих кораблей и этот клубок пронзают залпы лазеров, в нем летят и находят свою цель ракеты, здесь Вы забываете обо всем - и о "морковке" и о черно-белой графике. Перед Вами реальный, хорошо вооруженный противник - это вызов Вашему мастерству. Динамика игры, острота схватки и неповторяемость ситуаций делают возможным для вас эффект реального присутствия и вам уже не нужно художественное впечатление от богатства красок. Ваш мозг, увлеченный переживаниями, сам домыслит столько, сколько ему надо.
В этой статье мы коснемся только одной маленькой проблемы, которая связана с изображением на экране трехмерной векторной графики. Те из наших читателей, которые захотят скрупулезно изучить вопросы векторной (и не только векторной) графики прочитают книгу, а здесь мы рассмотрим один полезный алгоритм, который может быть принят на вооружение по крайней мере теми, кто использует свой "Спектрум" в практической работе, например при написании курсовых и дипломных проектов.
Сокрытие невидимых линий контура
При работе с трехмерной векторной графикой часто встает одна важная проблема -как изображать невидимые линии трехмерного объекта? Эта задача имеет непосредственное отношение к системам автоматизированного проектирования и наибольшее развитие получила именно в теории этих систем и, надо сказать, для ее решения привлекают довольно сложный аппарат из той области высшей математики, которая называется аналитической геометрией. Для нас с Вами, поскольку мы занимаемся обычной прикладной графикой, эту задачу можно несколько упростить. На данном этапе нас не интересует как изобразить невидимые линии - нам просто нужно их НЕ ИЗОБРАЖАТЬ.
Приемов и методов для достижения этой цели немало и мы рассмотрим один из наиболее простых, поддающийся несложной алгоритмизации.
Посмотрите на рис. 1. На нем изображен некоторый трехмерный ландшафт. Фактически это график функции:
Z = SIN (R)/R, где R = SQR (X*X + Y*Y).
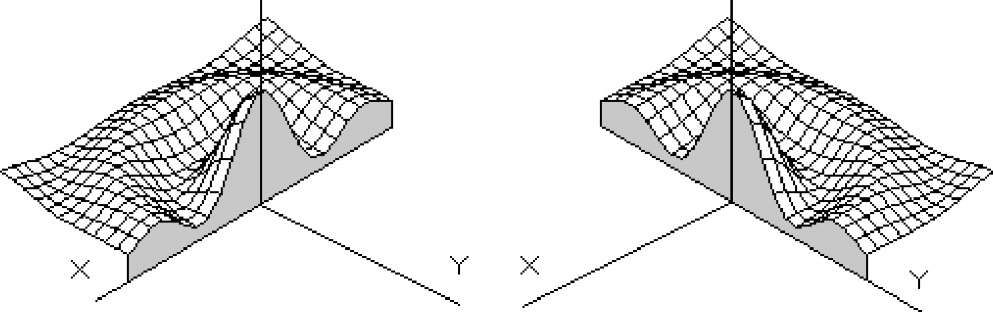
Рис.2 Рис.3
В своих экспериментах вы можете изменить эту функцию и поработать с другими. Важно только, чтобы она имела вид Z=f(x,y), т.е. чтобы была возможность составить однозначный алгоритм для вычисления координаты Z по заданным координатам X и Y. Самое интересное в этом графике - то, что скрытые детали - на самом деле скрыты. Все точки, которые находятся за гребнем или за вершиной - не показаны.
Алгоритм.
Давайте рассмотрим алгоритм, с помощью которого может быть достигнут желаемый эффект. Во-первых, надо отметить, что наша трехмерная поверхность изображается в два приема. На первом проходе изображаются все линии, параллельные оси X (рис. 2), а на втором проходе - линии, параллельные оси Y (рис. 3). Именно благодаря такому порядку изображения кривых и оказывается возможным скрыть невидимые детали.
Линии изображаются с некоторым шагом по X - Xh и по Y - Yh (см. рис. 4). Конечно, чем мельче шаг, тем детальнее будет проработано изображение, но слишком мельчить тоже не надо - существует некоторый оптимум, который можно установить методом проб и ошибок. Во всяком случае, параметры Xh=(Xmax-Xmin)/20 и
Yh=(Ymax-Ymin)/20
выглядят достаточно удачными.
Если какая-то часть вычерчиваемой в текущий момент линии оказывается за ранее проведенной кривой, то она не изображается и есть достаточно простой прием, который позволяет в программе принять такое решение.
Если мы выстраиваем изображение в виде семейства кривых, начиная от ближайшей к наблюдателю и удаляясь от него назад (т.е. идем от т.т. X2 и Y2 к т.т. X1 и Y1, как показано на рис. 4), то фактически те точки текущей линии, которые оказывается на экране ниже, чем точки ранее изображенных линий и являются невидимыми и должны быть скрыты.
Чтобы решить этот вопрос программно, мы создаем в оперативной памяти буфер размером 256 байтов, а дальше действуем следующим образом. Поскольку экран "Спектрума" имеет в ширину 256 пикселов, то мы будем считать, что он образован как бы из 256-ти узких однопиксельных вертикальных столбцов. Каждому столбцу отведем по одной ячейке памяти в нашем буфере и теперь всякий раз, когда будем печатать на экране точку, будем смотреть, что же содержится в буфере для данного столбца. Если то значение, которое есть там - меньше, чем вертикальная координата экрана, в которой мы будем печатать точку, то новая координата запоминается в данном буфере и точка печатается. Если же хранящееся там значение больше, чем текущая вертикальная координата позиции печати, то точка должна быть скрыта и не печатается, а значение в буфере не изменяется.
Y1
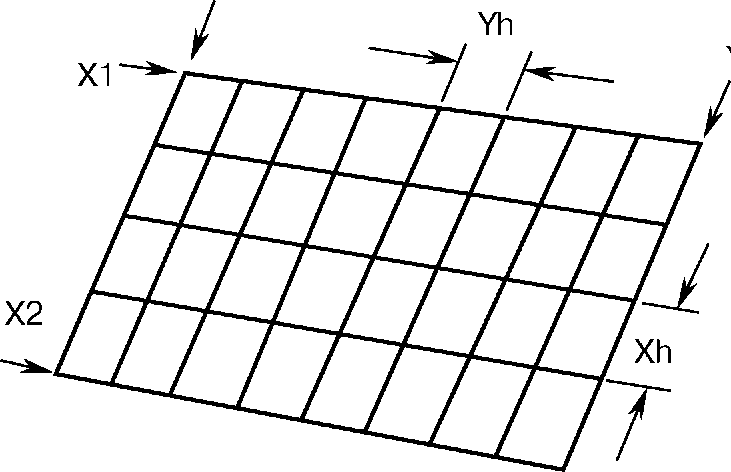
Y2
Рис. 4
Итак, алгоритм имеет следующий вид:
1. Задаем максимальные значения координат X2 и Y2.
2. Задаем минимальные значения координат X1 и Y1.
3. Определяем шаг по осям X и Y - Xh,Yh.
Xh =(Xmax-Xmin)/23
Yh=(Ymax-Ymin)/23
Мы специально делили здесь на "некруглое" число 23, а не на 20. Это помогает избежать прохождения через нулевую точку в том случае, если максимальные и минимальные параметры заданы симметрично относительно нуля. Все-таки неуютно себя чувствуешь, когда программа должна посчитать SIN(R)/R, когда R равно нулю. Хотя в принципе и этот случай можно было бы предусмотреть. Для тех, кто еще пока не изучал высшую математику, подскажем, что SIN(R)/R приближается к единице, когда R стремится к нулю.
4. Определяем масштаб по осям X и Y.
Для системы координат, показанной на Рис. 1...3 масштаб по X и Y - одинаков. Он зависит от ширины экрана и от угла между осями X, Y и осью Z. Для того, чтобы при любых допустимых значениях X и Y точка умещалась бы на экране, нам необходимо избрать масштаб:
(X2-X1) + (Y2-Y1)*255/SQR(3)*2
5. Задаем масштаб для оси Z (его можно менять).
6. Создаем буферный массив из 256 элементов, обнуляем их.
7. Начинаем строить семейство кривых, "параллельных" оси X. Организуем цикл по Y от Y2 до Y1 с шагом Yh.
8. Внутри этого цикла строим кривую "параллельную" оси X. Организуем цикл от X2 до X1 с шагом по Xh.
9. Внутри этого цикла для текущих значений X и Y определяем Z по заданной формуле функции.
10. Полученный результат для Z умножаем на масштаб, получаем координату Z для графика.
11. Выполняем преобразование систем координат. По трехмерным координатам X, Y, Z находим значения X и Y для плоскости экрана.
Формулы для этого преобразования будут зависеть от того, какую проекцию трехмерной системы координат на плоскость Вы изберете. Другими словами, они зависят от того, под какими углами Вы смотрите на трехмерный объект. Для случая, показанного на Рис. 1.. Рис. 3 подойдут формулы:
X = SQR(3)* (Y-X)/2 + 127
Y = Z - (Y+X)/2 + 87
12. Мы готовы поставить на экране точку в координатах x, y. Но сначала проверим, что есть в буфере для данной координаты x. Если там значение меньше, чем y, то точку x, y на экране ставим и значение y обновляем в буфере, а если оно больше, то точка - невидима, мы ее не ставим и значение в буфере не обновляем.
13. Вычислив экранные координаты точки x, y, мы готовы соединить ее линией с предыдущей точкой х', у' (если наша точка не первая). Хорошо бы для этого воспользоваться командой БЕЙСИКа DRAW или процедурой изображения отрезков в машинных кодах, но делать этого, к сожалению, нельзя. Причина в том, что этот отрезок (или его часть) может быть невидимым. Значит, надо строить его по точкам и для каждой точки проверять по буферу видима она или нет. Поэтому опять же надо организовать цикл для изображения отрезка по точкам.
14. Теперь надо определиться с параметром этого цикла. Он может изменяться по горизонтали (по x), а может и по вертикали (по у). Надо понять, что больше - приращение dx (равное x-x') или dy (равное у-у'). То, которое больше, и следует принять в качестве параметра цикла.
15. Определившись с параметром, организуем цикл и внутри него вычисляем координаты текущих точек, проверяем для них y сравнением с буфером и, если точка видима, печатаем ее и обновляем буфер, а если нет, то не печатаем и не обновляем буфер.
Здесь есть маленькая хитрость, которая несколько усложняет жизнь программисту. Дело в том, что эти соединительные отрезки можно проводить слева-направо, а можно и справа налево. В принципе это все равно, но есть один нюанс. Допустим мы будем их проводить слева направо. Все будет в порядке, пока нам не придется провести круто падающий отрезок. На один шаг по x для него происходит несколько шагов по y. И бывает так, что одной координате x соответствуют несколько точек y. Если бы мы рисовали этот отрезок снизу вверх, все было бы в порядке, а при движении сверху вниз (слева-направо) ранее напечатанная точка может "блокировать" печать следующих, забив в буфере свое координату. Поэтому круто падающие отрезки программа должна строить наоборот -справа-налево. Тогда отрезок становится как бы не "падающим", а "восходящим".
16. Соединив две точки на экране, переходим к очередной точке, отстоящей на Xh, и возвращаемся на шаг 8.
17. Построив кривую, "параллельную" оси X, переходим к следующей, отстоящей от нее на шаг Yh. Возвращаемся на шаг 7.
18. Когда все семейство кривых, "параллельных" оси X построено, половина дела
сделана. Теперь надо построить семейство кривых, параллельных оси Y.
19. Для этого сначала переинициализируем буфер, обнулив все его значения, а затем повторим все то же, что мы делали для семейства кривых, идущих вдоль оси X (шаги 7 - 18). Правда, при этом вместо шагов по X будем делать шаги по Y и наоборот.
10 LET xmax = 10: LET ymax = 10 20 LET xmin =-10: LET ymin = -10 30 LET xh = -(xmax-xmin)/23: LET yh = -(ymax-ymin)/23 40 LET scale = 255/SQR(3)*2/((xmax-xmin) * (ymax-ymin)) 50 LET zscale = 40
60 DIM c(256): FOR i = 1 TO 256: LET c(i)=0: NEXT i 70 FOR y=ymax TO ymin STEP yh: LET y1 = y*scale 80 FOR x=xmax TO xmin STEP xh: LET x1=x*scale 90 GO SUB 5000
100 IF x=xmax THEN GO SUB 8100: NEXT x
110 LET dy=yt-yold: LET dx=xt-xold
120 IF ABS(dy) >= ABS(dx) THEN GO SUB 6000: GO TO 140
130 GO SUB 7000
140 NEXT x
150 NEXT y
155 FOR i=1 TO 256: LET c(i)=0: NEXT i 160 FOR x=xmax TO xmin STEP xh: LET x1 = x*scale 170 FOR y=ymax TO ymin STEP yh: LET y1 = y*scale 180 GO SUB 5000
190 IF y=ymax THEN GO SUB 8100: NEXT y
200 LET dy=yt-yold: LET dx=xt-xold
210 IF ABS(dy) >= ABS(dx) THEN GO SUB 6000: GO TO 230
220 GO SUB 7000
230 NEXT y
240 NEXT x
250 STOP
4997 REM
4998 REM**********************************************
4999 REM
5000 LET r= SQR(x*x + y*y) : LET z = SIN(r)/r 5010 LET z = z*zscale
5020 LET xt=127+SQR(3)*(y1-x1)/2 5030 LET yt=87+z-(y1+x1)/2 5040 RETURN
5997 REM
5998 REM**********************************************
5999 REM
6000 IF dy<0 THEN GO TO 6100 6010 FOR i=0 TO dy
6020 GO SUB 6500 6030 NEXT i
6040 GO SUB 8100: RETURN 6100 FOR i=dy TO 0 6110 GO SUB 6500 6120 NEXT i
6130 GO SUB 8200: RETURN
6497 REM
6498 REM**************************************************
6499 REM
6500 LET xt = xold+dx/dy*i 6510 LET yt=yold + i
6520 GO SUB 8000: RETURN
6997 REM
6998 REM**************************************************
6999 REM
7000 IF dx<0 THEN GO TO 7100 7010 FOR i=0 TO dx
7020 GO SUB 7500 7030 NEXT i
7040 GO SUB 8100: RETURN 7100 FOR i=dx TO 0 7110 GO SUB 7500 7120 NEXT i
7130 GO SUB 8200: RETURN
7497 REM
7498 REM **************************************************
7499 REM
7500 LET xt=xold+i
7510 LET yt = yold+dy/dx*i 7520 GO SUB 8000: RETURN
7997 REM
7998 REM**************************************************
7999 REM
8000 IF yt > c(xt+1) THEN LET c(xt+1)=yt: PLOT xt,yt 8010 RETURN
8097 REM
8098 REM**************************************************
8099 REM
8100 LET xold=xt: LET yold=yt: RETURN
8197 REM
8198 REM**************************************************
8199 REM
8200 LET xold=xold+dx: LET yold=yold+dy: RETURN
СПИСОК ПРОГРАММНЫХ ПЕРЕМЕННЫХ
xmax - максимально-допустимое значение координаты X (задаетсяпользователем). ymax - то же для координаты Y.
xmin - минимально-допустимое значение координаты X (задается пользователем). ymin - то же для координаты Y. xh,yh - шаг между узлами сетки.
scale - масштаб по координатам X и Y (зависит от углов в пространстве, под которыми наблюдатель смотрит на трехмерный объект). Рассчитывается исходя из соображений оптимального использования плоскости экрана.
zscale - масштаб по оси Z (задается пользователем "по вкусу", но так, чтобы изображение по вертикали не вышло за пределы экрана). Возможно и автоматическое определение zscale в программе, во для простоты это не было сделано. с(256)- буферный массив на 256 элементов.
x1, y1 - отмасштабированные значения трехмерных координат X и Y. r - математический комплекс, нужный для вычисления Z. x,y - текущие трехмерные координаты X и Y в узлах сетки. xt,yt - текущие экранные координаты (двумерные). xold,yold - экранные (двумерные) координаты предыдущего узла. dx,dy - приращения экранных координат на очередном шаге (расстояние на экране между узлами).
Вот практически и весь алгоритм. Его описание выглядит страшнее, чем текст программы на БЕЙСИКе (см. распечатку), и это не случайно - ведь БЕЙСИК гораздо лучше подходит для описания алгоритмов и программистских идей, чем нормальный человеческий язык.
Конечно, скорость работы этой программы на БЕЙСИКе оставляет желать лучшего, но для иллюстрации самой концепции он неплох.
Мы попробовали - у нас получилось время работы программы что-то порядка пятнадцати минут, но тем не менее не пожалейте этого времени, поэкспериментируйте с
графиком.
Вы можете менять максимальные и минимальные значения X и Y. Вы можете менять масштаб по Z. В наших экспериментах мы получали кроме представленной на рис. 1 "шляпы" еще и "верблюда", "русалку", "замок в горах", "пепельницу", "ковер-самолет" и пр. и пр.
Более того, Вы можете менять и саму функцию, исследуя другие поверхности. Если Вы в приведенном нами примере замените вторую степень при X и Y на четвертую, то почувствуете, как холодок бежит по спине, когда компьютер изобразит очень натуральную свежую могилку с не менее натуральным каменным валуном в изголовье. Хочется пожелать Вам найти что-либо менее мрачное, особенно если вы работаете с компьютером по ночам.
Те же, кто предпочтут использовать для программирования машинный код, получат прекрасные результаты, но надо учесть, что программа выполняет большой объем чисто математических вычислений (это вообще характерно для трехмерной векторной графики). Здесь и масштабирование (чтобы график аккуратно занимал плоскость экрана) и пересчет из одной системы координат в другую (из трехмерной системы координат в двумерную систему координат плоскости экрана) и, конечно же, расчет самой функции Z=f(X,Y).
Процессор Z-80 не может оперировать с действительными числами, не может выполнять математических расчетов и здесь используют программирование в кодах калькулятора.
Пример программы в машинном коде мы здесь не даем, оставив для тех, кто интересуется, возможность ознакомиться с ним в книге. Подробный комментарий всех входящих процедур явится хорошим пособием для тех, кому необходимо программирование в кодах калькулятора.