3. ВЕКТОРНАЯ ГРАФИКА
Мы рассмотрели основы растровой графики и убедились, что
основным элементом растровых изображении является обыкновенная
точка (пиксел экрана). Все изображения получаются путем копиро-
вания пикселов заранее заданного шаблона в экранный Файл.
Принципы векторной графики существенно отличаются от прин-
ципов графики растровой, здесь основным элементом изображения
является прямая линия, а правильнее говоря отрезок прямой Все
графические объекты на экране получаются в виде ажурных кон-
струкций, созданных из набора отрезков, с их помошью могут по-
лучаться как плоские фигуры, так и проекции трехмерных тел.
Вы. уважаемые читатели, обратили, конечно, внимание на то,
что векторная графика в играх выглядит одноцветно, угловато и
художественными достоинствами очевидно не отличается. Так поче-
му же такие игры пользуются огромным успехом, с чем он связан?
Да, конечно, векторная графика выглядит на экране побед-
нее. чем многоцветная растровая графика, но у нее есть два
огромных преимущества. Во-первых, это очень быстрая графика.
Цикл освежения экрана и перестроения изображения происходит
намного быстрее, чем в программах с растровой графикой. Во-вто-
рых, это вычисляемая графика, то есть не надо хранить в памяти
компьютера заранее подготовленные экраны. Все изображения рас-
считываются по заданным алгоритмам и практически никогда не по-
вторяются. Благодаря этому вы можете иметь в таких программах
тысячи планетных систем, десятки возможных кораблей противника
и нескончаемое разнообразие игровых ситуации.
Вспомним программу "ELITE". Да, конечно, нужно иметь вооб-
ражение, чтобы принять угловатую "морковку" на экране Вашего
монитора за роскошный корабль "Fer-de Lance", нашпигованный чу-
десанн науки и техники и отделанный изнутри лучшими породами
дерева и самыми дорогими материалами. Но зато когда он врашает
ся вокруг всех собственных осей и при этом летит в пространст-
ве. изменяя свои координаты относительно Вашего корабля, а вы
вместе с ним при этом тоже перемешаетесь и маневрируете относи-
тельно планеты, звезды, станции и прочих кораблей, и этот клу-
бок пронзают залпы лазеров, в нем летят и находят свою цель ра-
кеты. здесь Вы забываете обо всем - и о "морковке" и о черно-
белои графике Перед Вами реальный, хорошо вооруженный против-
ник - это вызов Вашему мастерству. Динамика игры, острота
схватки и неповторяемость ситуации делают возможным для Вас
эффект реального присутствия и Вам уже не нужно художественное
впечатление от богатства красок. Ваш мозг, увлеченный пережива-
ниями. сам домыслит столько, сколько ему надо.
Итак» векторная графика - вычисляемая. Таким образом, ос-
новной программный аппарат, которым Вы должны располагать - это
процедуры для изображения отрезков прямых нежду точками с за-
данными координатами, математические процедуры, рассчитывающие
экранные координаты концов отрезков, в основе которых лежат из-
вестные Формулы из геометрии и тригонометрии, а также некоторые
процедуры для организации специальных приемов, таких как клип-
пирование. масштабирование, сокрытие линий невидимого контура и
затушевывание поверхностей, находящихся в тени (если задано на-
правление источника освешения).
Вот на этих технических приемах мы и остановимся. Единст-
венное. что мы не будем рассматривать - зто технику затушевыва-
ния теневых поверхностей, поскольку для того, чтобы определить,
какая поверхность трехнерного тела находится в тени относитель-
но заданного источника, необходимо применять математический
аппарат из области аналитической геометрии, а этот курс вузов-
ским и не входит в программу средней школы, под которую мы в
принципе подстраиваем наши книги. Те же читатели, которые зна-
комы с этой наукой, смогут подумав и сами реализовать необхо-
димые алгоритмы, особенно если учесть, что процедуру для запол-
нения замкнутого контура мы уже дали в прошлой книге - "Элемен-
тарная графика". Проблема сводится фактически не к тому, как
заштриховать контур, а к тому, чтобы определить только какой
контур надо закрашивать, а какой - нет. Надо также учитывать и
то, что эта техника очень редко применяется в динамичных играх
с быстроменяющейся ситуациеи. Этот прием больше подходит для
медленных игр стратегического или адвентюрного направления.
Мы не будем также рассматривать здесь вопросов анимаоии
изображений, хотя именно здесь векторная графика и проявляет
свои основные достоинства, оставив их для рассмотрения в
третьем томе нашей серии, который будет называться "Динаничес-
кая графика".
3. 1. Клиппирование изображений.
Выше мы сказали о том. что в основу векторной графики по-
ложено изображение тел и поверхностей в виде отрезков прямых.
И первое, о чем мы должны позаботиться - зто об изображении
ЛЮБЫХ отрезков прямых, а не только тех. которые нам позволяют
изображать ограниченные размеры экрана компьютера.
Рассмотрим конкретную игровую ситуацию, знакомую каждому,
кто хоть когда-нибудь играл в программу "Elite" Фирмы Firebird
Software или в другую подобную игру для космических ассов или
хотя бы слышал о них. Предположим, что перед Вами появился
враждебеный "Таргон" и открыл огонь на поражение. Ваши коорди-
наты примем за нулевые «XI=0; VI=0) и оии совпадают с центром
экрана (или с положением прицела Вашего корабля). Координаты
"Таргона" (X2.Y2) находятся в пределах экрана (Рис. 23 а).

Что представляет с точки зрения программиста изображение
вражеского лазерного лууа? это отрезок прямой линии, соединяю-
щей точки XI. Y1 и X2.Y2. Нарисовать такой отрезок очень неслож-
но. Можно воспользоваться процедурой ПЗУ, можно взять ту проце-
дуру. которую мы рассмотрели в книге "Элементарная графика",
можно, в конце концов, составить и свою, здесь нет никаких
проблем.
Теперь попробуем развернуть свой корабль вправо. Враг по-
кинул экран (Рис.236), его больше нет. мы спрятали "голову в
песок" и что? Прекратился обстрел? ничуть. Все также пронзают
черноту экрана яркие вспышки лазеров невидимого "Таргона". Что
представляет собой такая ситуация с точки зрения программиста?
Только то. что программа изображает отрезки прямых между точка-
ми. одна из которых (Ваш корабль) находится в области экрана, а
другая - нет. Это уже никакими процедурами ПЗУ и им подобными
сделать нельзя, а ситуация эта, как Вы должно быть понимаете,
очень распространена для программ, имеющих дело с векторной
графикой и ее надо рассмотреть особо.
для того, чтобы научиться рисовать что-либо в векторной
графике, необходимо сначала научиться рисовать обычные прямые
линии. Команда DRAW в БЕИСИКе вполне может Вам нарисовать такую
линию, если вся эта линия целиком укладывается на экране. А
теперь представин себе, что будет, если она НЕ УКЛАДЫВАЕТСЯ на
экране? Например, по командам:
PLOT 20.20
DRAW 250,250
Если вы попробуете это сделать, то безусловно получите
сообщение об ошибке "В integer out of ranee" и програнма пре-
кратит работу.
Может быть, все-таки лучше было бы. если бы программа не
прекращала работу, а изобразила хотя бы ту часть прямой, кото-
рая укладывается на экране. Эта концепция называется "клиппиро-
ваниен" изображения, т. е. из изображения "вырезается" та часть,
которая может быть нарисована на экране без проблем.
вполне возможен случаи, когда вся ваша предполагаемая ли-
ния не попадает на экран. В этом случае вся она будет клиппиро-
вана и ничего на экране вообше изображено не будет.
Давайте рассмотрим, как работает концепция клиппирования.
Взгляните на рис. гч
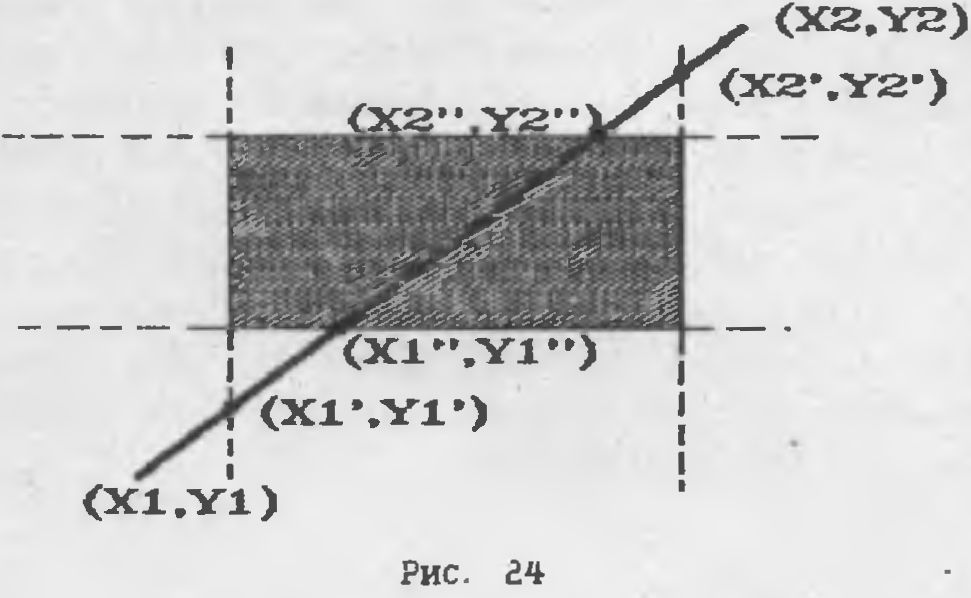
Заштрихованный прямоугольник - это наш экран. Предположим,
что Вы хотите изобразить отрезок прямой, соединяющей координаты
XI.Y1 и Х2.Y2. Чтобы клиппировать этот отрезок, мы должны так
приблизить друг к другу координаты его концов, чтобы получить в
конпе концов отрезок, вписываюшиися в пределы экрана, эта опе-
рация выполняется в четыре приема.
Сначала мы отыскиваем точку XI'Y1'. в которой наш отрезок
пересекает левую границу экрана, затем мы отыскиваем точку
XI".VI". в которой отрезок пересекает нижнюю границу экрана и
потом, соответственно, точки X2'.Y2' и X2",Y2". как видите,
отрезок от XI". VI" до X2".Y2" полностью вписывается в пре-
делы экрана компьютер'а.
Эта же технология должна работать и если клиппируемая ли-
ния будет располагаться по-другому, а не так. как показано на
Рис.24. Т.е. где бы ни лежала точка XI. Y1. мы должны сначала
рассчитать xi'.y1' и передвинуть точку к ближайшей правой или
левой границе экрана ТОЛЬКО В ТОМ СЛУЧАЕ, если она лежит от
экрана слева или справа. В противнон случае ее следует оставить
тан. где она есть. После этого можно переходить к расчету
XI".Y1"« передвигая точку ТОЛЬКО ЕСЛИ ЭТО НЕОБХОДИМО (если
она лежит ниже или выше пределов экрана). То же самое относится
и к точке Х2. Y2.
Необходимо предусмотреть варианты, когда вся линия лежит
вне пределов экрана. Так. если координаты и начала и конца
отрезка лежат слева от экрана, то кпиппировать в этой линии
нечего и изображать ее не надо. То же самое, если координаты
обоих концов лежат справа, сверху или снизу от экрана.
Впрочем, могут быть и еше некоторые положения отрезка, при
котором он не проходит через экран и которые идентифицировать
гораздо более сложно. На Рис. 25 показаны примеры таких отрез-
ков.
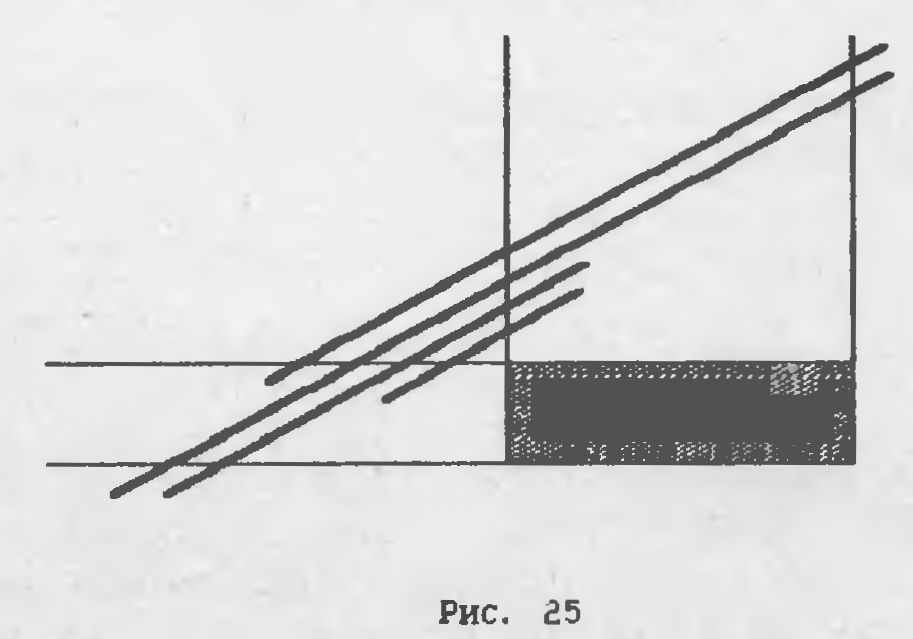
Если все. что Ван известно о таких линиях - это только
координаты начала и коииа, то весьна сложно создать алгоритм,
по которому программа будет принимать решение о том. проходит
или нет линия через экран. К счастью, есть вариант обхода про-
блемы. Все. что для этого нужно, это рассчитать XI". Y1" и
X2".V2" по вышеописанной методике и. если после этого, какая-
либо из точек по-прежнему выходит за пределы экрана, то и вся
линия не лежит в области экрана и ие должна изображаться.
Окружности.
Окружности могут изображаться, как ряд очень малых отрез-
ков прямых, что дает впечатление непрерывной замкнутой кривои
линии. Другими словами, вместо изображения окружности мы можем
рисовать правильный многоугольник с большим числом очень малых
сторон. Чем больше количество сторон, тем больше наш много-
угольник похож на настоящую окружность. В идеале количество
сторон следует принимать таким, чтобы оно было кратно четырем,
тогда результирующее изображение получится симметричным.
В чисто практических целях можно приближенно определить
количество сторон многоугольника для окружности заданного ради-
уса с помошью эмпирическом функции
n = PI»SQR(R). где R - радиус.
для той разрешающей способности, которую имеет "Спектрум",
эта Формула работает очень хорошо:
|
("ВТ——
R |
П |
R |
п |
|
10 |
12 |
100 |
32 |
|
20 |
16 |
160 |
40 |
|
30 |
16 |
200 |
44 |
|
40 |
20 |
256 |
52 |
Если же теперь мы подвергнем каждый отрезок процедуре
"клиппирования". которая была описана выше, и не будем рисовать
те отрезки или их части, которые не лежат в области экрана, то
в результате получим клиппированную окружность. Только та часть
окружности, которая проходит через экран, будет изображена, все
же остальное будет проигнорировано.
Развивая этот принцип далее, мы сможем применить ту же
л
идею и для изображения других типов кривых, а не только окруж-
ностей. например для эллипсов (Рис.26).
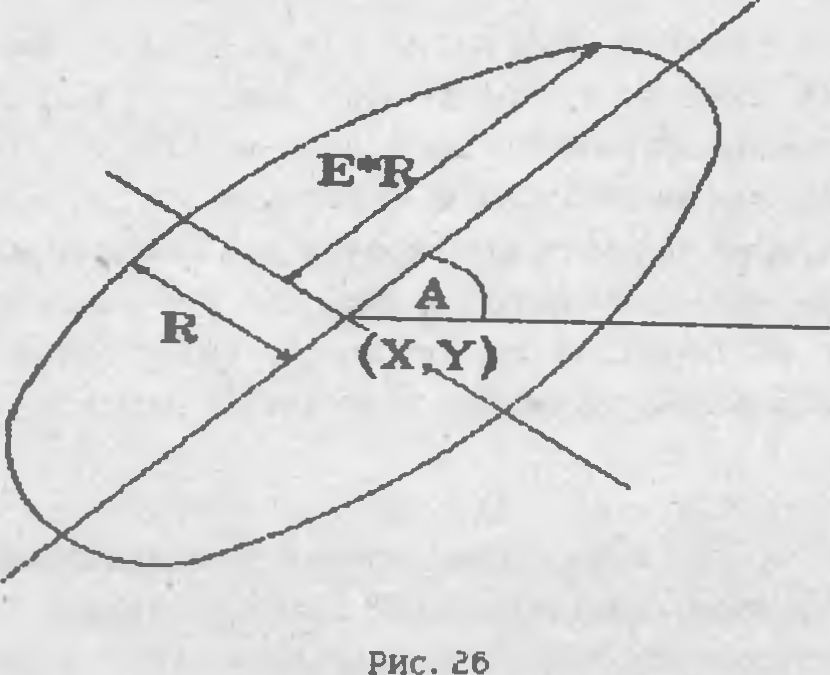
X и V - координаты центра эллипса. R - размер его малой
полуоси. е - эксцентриситет, он равен отношению большей полуоси
эллипса к меньшей и всегда больше единицы. А - угол в радианах
между большей полуосью эллипса и горизонталью.
Ниже мы привели процедуры в машинных кодах, которые реа-
лизуют описанные приемы.
FN S(Xl.Yl.Х2.Y2) - клиппированные прямые;
FN С(Х.Y.R) - клиппированные окружности;
FN Е(Х. Y. R. Е. А) - клиппированные эллипсы.
Посмотреть как они работают. Вы можете, набрав небольшую
демонстрационную программу на БЕИСИКе. Вместо многоточия в опе-
раторах USR...... следует подставить конкретные адреса, соот-
ветствующие точкан входа в процедуры, вычерчивающие клиппиро-
ванные отрезки, окружности и эллипсы.
10 DEF FN S(A, B.C. D) : USR........
20 DEF FN C(X,Y. R) = USR ........
30 DEF FN E(X.Y.R.E.A) = USR........
100 FOR К • О TO PI STEP PI/20
110 RANDOHIZE FN E( 128. 66. 60. 2. K)
120 NEXT К
130 FOR K- 60 TO 120 STEP 20
140 FOR J= 0 TO 4
150 LET A1 = (2* j/5 + 0.5) «PI
160 LET A2 = (2« (J*2)/5 ♦ 0. 5) "PI
170 RANDOHIZE FN S(128 ♦ K»COS Al. 88 + K«SIN Al.
128 ♦ K«C0S A2. 88 ♦ K»SIN A2)
180 NEXT J
190 RANDOHIZE FN С(128.88. К)
200 NEXT К
В своей работе процедуры активно используют встроенный
калькулятор, при этом им необходимы двадцать ячеек внутренней
памяти калькулятора, стандартно калькулятор имеет только шесть
ячеек памяти. Дополнительную память необходимо создать в рабо-
чем пространстве, используя команду процессора RST ЗОН. Кроме
этого, нужно установить системную переменную МЕН. определяющую
положение ячеек памяти калькулятора так. чтобы она указывала на
эту дополнительную память. После работы процедур необходимо
восстанавливать значение НЕМ в первоначальное (5С92Н). что и
сделано в программе перед выходом.
Вот раскладка этих ячеек памяти калькулятора:(первые де-
сять служат для клиппирования отрезков прямых, последующие
десять служат для работы с окружностями и эллипсами).
Ячейка Параметр Комментарий
НО Pi Координата X точки начала отрезка минус
127. 5. т. е. эта координата "привязана" к
центру экрана.
Hi Qi Координата V точки начала отрезка минус
87. 5
иг р£ Координата x коныа отрезка минус 127. 5.
МЗ йг Координата V конца отрезка минус 67. 5.
ГМ S1 Вспомогательный флаг, характерзуюшии по-
ложение точки XI относительно экрана.
Если точка слева от экрана, то Si=-l;
если точка справа от экрана, то Si = i;
если XI принадлежит экрану, то Si = 0.
Ц5 Т1 Вспомогательный Флаг, характерзуюшии по-
ложение точки VI относительно экрана.
Если точка ниже экрана, то Т1=-1;
если точка выше экрана, то Tl = l:
если VI принадлежит экрану, то Ti-Q.
Мб S2 то же. что и S1. но для координаты Х2 конца
отрезка.
М7 Т2 то же. что и Т1. но для координаты V2 коииа
отрезка.
М8 127.5 Постоянное число - половина ширины экрана.
М9 67.5 Постоянная - половина высоты экрана.
MA E»R Размер большей полуоси эллипса.
MB r Меньшая полуось эллипса (для окружности -
радиус).
МС COS(А) характеризуют наклон большей полуоси эллип-
MD SIN(А) са к горизонтали.
ME Ai Текушее значение угла наклона А.
MF INCR Шаг. с которым наращивается текушее значение
угла наклона а.
MlО Р экранная х-координата текущей изображаемой
точки эллипса (окружности).
Mil Q экранная Y-координата текушей изображаемом
точки эллипса (окружности).
Ml2 X экранная Х-координата центра эллипса.
Ml 3 V экранная v-координата центра эллипса.
Если Вы входите в процедуры из БЕИСИКа. как показано в
демонстрационной программе, то передача параметров осуществля-
ется через аргументы пользовательских Функции FN о, но если
Вы хотите войти в эти процедуры из машинного кода, то иадо
самим позаботиться о передаче параметров, в этом случае они
должны быть предварительно помешены на вершину стека калькуля-
тора (обязательно в указанном порядке):
FN S(. . . ) - XI. VI, X2, va
FN E(. . . ) - X. V. R. E. A
Поскольку окружность это частный случаи эллипса, у которо-
го эксцентриситет равен единице, а угол наклона большой полуоси
равен нулю, то для изображения окружности из машинного кода
можно пользоваться той же точкой входа, что и для эллипса, а на
вершине стека калькулятора необходимо предусмотреть последова-
тельность:
X. Y. R. 1. о
Использованные процедуры.
Процедуры ПЗУ
RST ЗОН - процедура служит для создания дополнительных
ячеек памяти калькулятора, на каждую ячейку выделяется по пять
байтов, суммарное количество байтов, которое нужно выделить для
памяти калькулятора устанавливается перед вызовом RST зон в
регистровой паре ВС. Важно также иметь ввиду, что после работы
этой процедуры регистровая пара DE указывает на первый байт
выделенной дополнительной области.
STACK_NUM (ЗЗВ4Н=13236 DEC) - процедура помешает на верши-
ну стека калькулятора интегральное (пятибайтное) число, которое
начинается с адреса, на который указывает регистровая пара hl.
Применяется для ввода на стек тех параметров, которые пользова-
тель подставил в пользовательской Функции FN о.
FP_T0_A (£DD5H=11733 DEC) - процедура снимает с вершины
стека калькулятора действительное число, конвертирует его в
целое и переносит в аккумулятор микропроцессора. Если получае-
мое при этом число больше чем 255, включается Флаг переноса -
С. О знаке числа можно судить по состоянию Флага нуля - Z. если
число положительное или ноль, флаг Z включен, а если отрица-
тельное - выключен.
PLOT (22DCH = 8934 DEC) - при этой точке входа процедура
PLOT снимает со стека два верхних значения и. считая, что это
экранные координаты точки У и X, напечатает точку в данных
координатах.
LINE.DRAV (2477Н = 9335 DEC) - процедура рисует отрезок
прямой от последней изображенной на экране точки к точке, коор-
динаты которой отстоят от последней на величину смешения, кото-
рое задано на вершине стека калькулятора.
STACK.A (2D26H = и560 DEC) - процедура переводит целое
число, содержащееся в аккумуляторе, в действительное число и
помешает его на вершину стека калькулятора.
Процедуры программы.
MAIN - головная процедура, с которой начинается вся рабо-
та. Отсюда распределяется работа по прочим процедурам програм-
мы.
SET_UP - процедура создает необходимое количество ячеек
памяти калькулятора но или 20) и помешает на вершйну стека
калькулятора те параметры, которые были заданы в функции поль-
зователя FN О при вызове программы.
CLIP - головная процедура для изображения одного клиппиро-
ванного отрезка. Здесь рассчитываются координаты начала и конца
отрезка относительно центра экрана (PI. Ql. Р2. Q2) и устанав-
ливаются в соответствующие ячейки памяти калькулятора МО... МЗ.
здесь же выставляются постоянные в ячейках ив. М9, определяется
возможность изображения части отрезка на экране и. если это
возможно, отрезок рисуется вызовом процедур PLOT и LINE_DRAW из
системного ПЗУ компьютера.
PARAMS - процедура, которая по заданным координатам начала
и конца отрезка определяет состояние Флагов Sl.Ti.S2.T2 и зано-
сит их в соответствующие ячейки памяти калькулятора Ml... М7.
C0NV.x - процедура рассчитывает координаты пересечения на-
шего отрезка с горизонтальными границами экрана Pi'.01' или
P2',Q2'.
CONV.y - процедура рассчитывает координаты пересечения
нашего отрезка с вертикальными границами экрана Pi".Qi" или
F2". Q2".
EL_hain - головная процедура для изображения клиппирован-
ного эллипса (или окружности). Здесь инициализируются ячейки
памяти калькулятора, связанные с эллипсани и окружностями, про-
изводится аппроксимация до Н-угольника и организуется цикл изо-
бражения сторон n-угольникэ с цомошыо процедуры рисования клип-
пированных отрезков CLIP.
NEXT.POIHT - процедура вычисляет экранные координаты XI
или Х2 и VI или V2 для текущей точки эллипса по заданным R, Е.
А. Al. Конечная цель процедуры вычислить:
XI(Х2) = X»E«R«C0S(A1)«COS(A)-R«SIN(A1)»SIN(А)
Y1(Y2) = V+E«R«C0S(A1)«SIN(A)♦R«SIN(Al)«COS(A)
Процедура MAIN
Код Метка Мнемоника Комментарии (стек калькулятора)
013200 LINE LD ВС. 0032 ; 32Н = 50 DEC. Это подготовка к
; созданию 10 ячеек памяти каль-
.кулятора ino 5 байтов на каж-
; дую) .
CD???? CALL SEt_UP .Вызов процедуры SET_UP.
CD???? CALL CLIP .Вызов процедуры рисования клип-
;пированного отрезка.
1615 JR EXIT ;Переход на Финишные операции.
о16400 CIRCLE LD ВС.0064 ; Точка входа для изображения
; окружности. 64Н = 100DEC - это
,подготовка к созданию 20-ти
; ячеек памяти калькулятора.
CD???? CALL SET_UP ;Вызов процедуры SET_UP.
EF RST 26H .'Включение калькулятора:
; (X. У. R).
А1 const_1 ;Т. к ОКРУЖНОСТЬ - это эллипс. У
.которого эксцентриситет равен
;единице, то на вершину стека
;заслали число 1.
. (X. tf. R. 1)
АО const.О .заслали о на вершину стека -
^ .это угол наклона большой полу-
; оси эллипса.
; (X, V. R, 1, О).
36 endcalc ;Выключение калькулятора.
1606 JR ELL-2 ;Переход на рисование эллипса.
016400 ELLIPS LD ВС.0064 .Точка входа для изображения эл-
липса. 64Н в ВС - это подготов-
; ка к созданию 20 ячеек памяти
; калькулятора.
CD???? CALL SET_UP ; Вызов процедуры SET_UP.
CD???? ELL_2 CALL EL_MAIN; Вызов головной процедуры рисо-
. вания эллипса.
21925С EXIT LD HL.МЕМВОТ;Восстановление системной пере-
22685С LD (HEH).HL ;меннои МЕН перед выходом из
; программы.
215627 LDHL.2756 :ВНИМАНИЕ! Многие ПРОпедУРЫ
.калькулятора "портят" регистро-
вую пару H'L' (альтернативную).
;Если в ней не восстановить ис-
; ходное значение (2758Н), то
. возврат в ббисик не получится.
. Все. кТо работают с машинным
;кодом, никогда не должны
; забывать об этом.
В9 ЕХХ . пара HL стала альтернативной.
С9 RET " ;Конец работы программы и выход
; в БЕЙСИК.
процедура set.UP
Код Метка Мнемоника Комментарий
f7 SET.uf RST 30 ; Создание в рабочей области про-
; странства для размешения допол-
;нительных ячеек памяти кальку-
; лятора.
ED53685C LD (MEM),DE ; В системной переменной MEM
;устанавливается адрес нового
;места расположения памяти
.калькулятора.
i£A0B5C LD HL, (DEFADD); HL указывает на первый параметр
; функции пользователя FN ().
23 SU.LOOP INC HL ; Пропустили имя этого параметра.
23 INC HL ; Пропустили символ CHR 14, за
; которым следуют 5 байтов число-
;вого значения параметра.
CDB433 CALL STACK.NUM ; Вызов процедуры ПЗУ, которая
;скопирует значение, на которое
;указывает HL. на вершину стека
;калькулятора.
7Е LD A. (HL) ;Проверим, что за байт стоит
;после принятого параметра.
23 INC HL ;Пропустим этот байт.
FE2C CP 2С .Не запятая ли это? код запятой
. равен 2С.
26F5 JR Z. SU.LOOP; Если это запятая, то значит не
; все параметры приняты из FN о
;и следует возврат на SU.L00P.
С9 RET , В противном случае возврат в
;вызывающую процедуру.
Процедура CLIP
Код Метка Мнемоника комментарии (стек калькулятора)
EF CLIP RST 28 (Включение калькулятора. После
;Того, как отработала процедура
.SET.UP. мы имеем на вершине
. стека XI. Y1. иг. Y2.
34372F stK.data 87.5 ; Заслали на вершину число 67,5.
; (XI. Y1, Х2. Y2. 87.5).
С9 store_M9 ; Записали его в ячейку М9.
; (XI, Yl. Х2. Y2. 87.5).
03 subtract .Вычитание Q2 = Y2-87.5;
; (XI. Yl. Х2. 02)
СЗ store_M3 ;запомнили Q2 в ячейке ИЗ.
02 delete Удаление числа с вершины;
; (XI. Yl, Х2)
34377F stK_data 127.5 ;Заслали на вершину число 127,5.
; (XI. VI. Х2, 127. 5).
С8 store.Me ;записали его в ячейку М8.
; (XI, Yi. Х2. 127. 5).
03 subtract ; Вычитание Р2 = Х2-127.5;
, (XI. Yl. Р2)
С2 store_H2 .Запомнили Р2 в ячейке Н2.
02 delete ;Удаление числа с вершины;
; (XI. VI)
Е9 recall_Н9 ;Вызов числа из М9;
. (XI. Y1. 87. 5)
03 subtract ;(XI. 01)
Cl store.Hl ;Запись в ячейку Mi;
02 delete ; (XI).
Е8 recall_мв .Вызов числа из М8;
; (XI. 127.5).
03 subtract ;(Pi)
CO store.МО ; Запись в ячейку МО.
02 delete ;Стек пуст.
• 38 endcaic : Выход из калькулятора.
CD???? CALL PARAMS ; Устанавливаем параметры
; SI. Tl. S2. T2.
EF RST 28 ;Включение калькулятора.
E4 recal1.M4 :Ha вершине: Si.
Еб recall.Мб ;На вершине: Si. S2.
04 multiply :На вершине: S1«S2.
Ai const.one ;На вершине: Sl»S2. 1.
03 subtract ;На вершине: S1*S2-1.
Е5 recal1_М5 ;(S1«S2-1. Tl)
Е7 recal1.М7 ;(Sl»S2-l. Tl. T2)
04 multiply ; (SI*S2-1. T1»T2)
Al const.one ;(S1»S2-1. T1»T2, 1)
03 subtract ;(S1«S2-1. Tl»T2-l)
04 multiply
38 endcaic ; Выключение калькулятора.
CDD52D CALL FP.TO.A ;Результат расчета комплекса
;iSl*S2-l)*(Tl»T2-i) помешается
; в аккумулятор.
С8 RET Z ; Этот комплекс не может иметь
;положительного значения вообше
; никогда и потому Флаг 7. может
;включиться только если он равен
;нулю, а это бывает тогда и
; только тогда, когда либо S1 = S2,
;либо Т1=Т2. В этих случаях весь
; отрезок лежит слева или справа
:или сверху или снизу от экрана.
.В этом случае его рисовать не
; надо и' выполняется возврат в
; вызывающую программу.
EF RST 28 ; Включение калькулятора.
Е4 recal1.М4 ;(Si)
30 eq.zero ;isi=0?>
0010 jump.true, CLIP_1 ; переход иа CLIP_i. если Si=0
E4 recall M4 ;(Sl>
38 endcalc t:Выключение калькулятора, на
;вершине стека оставили S1.
CD???? CALL COHV_X ;Расчет Ql'. PI'.
EF RST 28 . Включение калькулятора. На вер-
;шине стека Ql'. Pi'.
СО store_H0 jPi* запоминается в но вместо Pi
02 delete
Cl store.Hl ;Ql* запоминается в Hi вместо Ql
02 delete г Стек пуст.
38 endcalc :Выключение калькулятора.
CD???? CALL PARAMS ;Перейдя к новый значениям коор-
динат начала отрезка, мы должны
;снова пересчитать параметры S. Т
Е4 RST 28 ; включение калькулятора.
Е5 CLIP.l recall_М5 ; Т1*.
30 eq_zero ;Т1'=0?
OOOB jump_true. CLIP_2 ; Переход на CHP_2. если Ti'=0.
E5 recall_M5 ;Tl*.
38 endcalc ;Tl*.
CD???? CALL COKV_Y :Расчет Ql". Pi".
EF RST 28 ;Ha стеке- Qr'.Pi".
CO store.MO :B МО теперь Pi".
02 delete ;Ha стеке: Ql".
Cl store_Mi : В Ml теперь Ql".
02 delete .Стек пуст.
Еб CLIP_2 recall_M6 :S2.
30 eq_zero ;S2=0?
0010 Jump_true. CLIP_3 : Переход, если S2 = 0.
Еб recall_M6 :S2-
38 endcalc ;S2.
CD???? CALL CONV_X ;Расчет 02'.P2'.
EF RST 28 ;на стеке 02'. P2
C2 store_M2 ;в M2 теперь P2'.
02 delete ;Ha стеке: 02'.
C3 store_H3 ;B ИЗ теперь 02'.
02 delete ;Стек пуст.
38 endcaic
CD???? CALL PARAMS ;Пересчет параметров S2' и T2'
EF RST 28
E7 CLIP_3 recal1.M7 ;T2'.
30 eq_zero ,T2'=o?
OOOB jump_true. CLIP_4 ;Переход, если T2'=0.
E7 recall_M7 ;T2'.
38 endcaic ,T2'.
CD???? CALL CONV.Y ; Поиск 02". P2".
EF RST 28 ;Q2".P2".
C2 store_M2 ; В M2 теперь P2".
02 delete ;Q2".
C3 store_M3 ;В M3 - Q2".
02 delete ;Стек пуст.
38 CLIP.4 endcaic
CD2580 CALL PARAMS ; Пересчет S1".S2",T1",T2".
EF RST 28 iВключение калькулятора.
E4 recal l_M4 ; Si".
E5 recall -M5 ; Sl". Tl".
07 or ;Sl" OR Tl".
E6 recal1_M6 .Sl" OR T1-.S2".
07 or ; Sl" OR Tl" OR S2".
E7 recall_M7 iSl" OR Tl." OR S2", T2".
07 0Г .Sl" OR Tl" OR S2" OR T2".
38 endcaic
CDD52D CALL FP.TO.A;В аккумулятор пересылается
;результат логической операции
; Sl" OR Tl" OR S2" OR T2".
A7 AND A
CO RET NZ ;Если Флаг нуля не включен.
; значит никакая часть отрезка не
.принадлежит экрану и следует
; возврат в вызывающую процедуру
EF RST 28 ; Включение калькулятора.
E2 recal1_М2 ; Вызов Р2".
Е8 recal1_М8 :Р2".127.5.
А2 COnst_half . Р2", 127.5. 0.5.
OF add ;P2". 128.
C8 store_M8 ;теперь в не число 128.
OF add ;P2" + 128.
27 int ; X2".
C2 store_M2 ;Теперь в иг координата X2".
ЕО recail_MO ;X2".Pi".
E8 recall_H8 ;X2". Pi". 128.
OF add ;X2". Pl"*128.
27 int : X2". XI".
CO store HO ;Теперь в Hi координата XI".
03 subtract ;X2"-Xi".
E3 recall_M3 ;X2"-Xl". Q2"
E9 recall_M9 ;X2"-X1". Q2". 87.5
A2 const-half :X2"-X1". Q2". 87.5. 0.5
OF add ;X2"-X1". Q2". 88
C9 store_H9 ;B H9 число 88.
OF add ;X2"-X1". Q2"+88
27 int ;X2"-X1". Y2"
C3 store_H3 ;в ИЗ координата Y2".
El recal1_H1 ;X2"-X1". Y2". Ql"
E9 recal1_H9 ;X2"-X1". Y2". Ql". 88
OF add ;X2"-X1". Y2". Ql"*88
27 int ;X2"-X1". Y2". Yl"
Cl store.Ml ;B Hi координата Yl".
03 subtract ;X2"-X1". Y2"-Y1"
EO recal1_M0 ;X2"-X1". Y2"-Y1". XI"
El recal1_M1 ;X2"-X1". Y2"-Y1". XI". Yl"
38 endcalc ;V нас на вершине стека кальку-
лятора получилась следушая
конфигурация: верхние два
; вложения выражают координаты
;точки начала экранной части
; отрезка, а нижние два вложения
;выражают "смешение" координаты
;конца клиппироваНного отрезка
;относительно его начала.
CDDC22 CALL PLOT ;Вызов процедуры ПЗУ. которая
.напечатает точку с координатами
;Xi",Yl" и снимет два верхних
; вложения со стека калькулятора.
С37724 JP LIHE_DRAW; переходом на процедуру ПЗУ
; line.DRAW завершается эта об-
ширная процедура. line.draw
; вызовет draw.lihe (24в7н). на-
рисует на экране отрезок и вы-
;полнит завершающий возврат в
;вызывающую процедуру.
Процедура PARAMS
Код метка мнемоника Комментарий (стек калькулятора)
EF PARAMS RST 28 ; Включение калькулятора.
ЕО recal1_МО ;Х1
31 duplicate ;XI. XI
2А abs ; XI. ABS(Xl)
Е8 recal1_M8 ; XI. ABS(Xl). 127.5
03 subtract ; XI. ABS(Xl) - 127.5
37 it_zero ;X1. ABS(X1)>127. 5?
0003 jump.true, PAR_l ; XI. переход, если ABS(X1)>127. 5
02 delete ;
AO const.zero ;0
29 PAR_1 sin ! Sl
C4 store.Ml ;B m хранится Sl.
02 delete ;
El recall_Ml :Yi
31 duplicate ;Y1. Yl
2A abs ; Yl. ABS(Yl)
E9 recal1_M9 ;Yl. ABS(Yl). 87.5
03 subtract ; Yl. ABS(Yl) - 87. 5
37 et_zero ; Yl. ABS(Y1)>87. 5?
0003 jump_true. PAR_2 ; Yl. переход, если ABS (Yl) >87. 5
02 delete ;
AO const.zero :0
29 PAR_2 sen ; Т1
С5 store_M5 ;В М5 хранится Т1.
02 delete ;
Е2 recal1.М2 .Х2
31 duplicate ; X2. Х2
2А abs : Х2. ABS (Х2)
Е8 recal1_И8 ;X2. ABS(X2). 127.5
03 subtract ; X2. ABSIX2) - 127.5
37 et.zero ; X2. ABS(X2)>127.5?
0003 jump_true.PAR_3 ;X2> переход, если ABS(X2)>127. 5
02 delete ;
AO const_zero ;0
29 PAR.3 sen ;S2
C6 , store_M6 ;B Мб хранится S2.
02 delete ;
E3 recal1_M3 ;Y2
31 duplicate ;Y2. Y2
2A abs ; Y2. ABS(Y2J
E9 recal1_M9 . Y2. ABS(Y2). 87.5
03 subtract ; Y2. ABS(Y2) - 87.5
37 gt_zero ; Y2. ABS(Y2) >87. 5?
0003 jump_true. PAR.4 ; Y2. переход, если ABS(Y2)>87. 5
02 delete ;
AO const_zero ;0
29 PAR-4 sen ; T2
C7 store_M7 ; в M7 хранится T2.
02 delete
38 endcalc ;
C9 RET :Выход из процедуры.
Процедура C0NV.X
Код метка Мнемоника Комментарий (стек калькулятора)
EF CONV_x RST 28 : Включение калькулятора.
;На стеке: S
Е8 recal1_М8 ; s. 127.5
04 multiply :127.5«S
31 duplicate ; 127. 5«S. 127. 5«S
E0 recal 1_H0 ; 127. 5*S. 127. 5«S. XI
03 subtract ; 127. 5»S, 127. 5«S - XI
E3 recal 1_M3 ; 127. 5«S. 127. 5»S - XI. Y2
El recal 1_M1 ; 127. 5«S. 127. 5»S - XI. Y2. Y1
03 subtract i 127. 5»S. 127. 5»S-X1. Y2-Y1
04 multiply ; 127. 5»S. (127. 5«S-X1)M¥2-Y1>
E2 recal 1.И2 ; 127. 5»S. (127. 5»S-X1) MY2-Y1). X2
EO recal 1.MO ; 127. 5«S, (127. 5«S-X1) »(Y2-Y1).
:X2. XI
03 subtract ;127.5«S. (127. 5»S-X1)»(Y2-Y1).
;X2 - XI
05 divide ; 127. 5»S, (127. 5«S-X1)»(Y2-Y1)/
;(X2-X1)
El recall_Ml i 127. 5«S. (127. 5«S-X1) « (Y2-Y1)/
;(X2-X1). Y1
02 add ; 127. 5»S. Yl*(127. 5»S-X1)«(Y2-
;-Y1)/(X2-X1)
01 exchanee ;Yl+(127.5»S-X1)»(Y2-Y1)/(X2-X1)
;. 127. 5«S
38 endcaic
C9 RET
Процедура COHV_Y
Код Метка Мненоника Комментарий (стек калькулятора)
EF COHV_Y RST 28 i Включение калькулятора.
;На стеке: т
Е9 recal 1_М9 ; Т. 87.5
04 multiply ;87.5»Т
31 duplicate ; 87. 5*Т. 87. 5»Т
El recall_Ml ;87. 5»Т. 87. 5»Т, Y1
03 subtract ;87. 5»Т. 87. 5»Т - Y1
E2 recall_H2 ; 87. 5»T. 87. 5»T - Yl. X2
EO recall-HO ; 87. 5»T. 87. 5»T - Yl. X2. XI
03 subtract : 87. 5«T. 87. 5*T-Y1. X2-X1
04 multiply : 87. 5»T. (87. 5«T-Y1)»(X2-X1)
E3 recal 1_ИЗ ; 87. 5«T. (87. 5«T-Y1 И (X2-X1), Y2
El recall^Hl ; 87. 5«T. (87. 5«T-Y1) MX2-X1).
:Y2. Yl
03 subtract ; 87. 5»T. (87. 5«T-Yl) » (X2-X1).
;Y2 - Yl
05 divide ; 87. 5»T. (87. 5»T-Y1)»(X2-X1)/
;(Y2-Y1)
Ep recall_H0 ; 87. 5»T. (87. 5»T-Y1 > « (X2-X1)/
:(Y2-Y1). XI
02 add ; 87. 5*T. XI ♦ (87. 5«T-Y1) « (X2-
:-XI)/(Y2-Y1)
38 endcalc
C9 RET
Процедура EL.MAIK
Код Нетка Мнемоника Комментарий (стек калькулятора)
EF EL_HAIN RST 28 ; Включение калькулятора.
.На стеке: X. Y. R. Е. А
31 duplicate ; X. Y. R. Е, А, А
20 COS ; X. Y. R. Е. A. COS (А)
СС store.MC ; ячейка памяти НС хранит COS(А)
02 delete ;Х. Y. R. Е. А
IF Sin ; X. Y, R. Е. SIHCA)
CD store_MD : Ячейка памяти MD хранит SIN(А)
02 delete ;Х. Y. R. Е
01 exchanie ; X. Y. Е. R
СВ store_MB ;Ячейка памяти MB хранит R
04 multiply . X. Y. E»R
СА store_HA ;Ячейка памяти МА хранит E»R
02 delete ;X. Y
D3 store_Mi3 .Ячейка памяти Mi3 хранит Y
02 delete ;X
D2 store_Mi2 ;Ячейка памяти M12 хранит X
02 delete ;Стек пуст.
АО const_zero ; О
СЕ store.ME : В ячейке ME выставляется ноль.
02 delete ;Стек пуст.
ЕВ recal1_МВ .R
2A abs ;ABS(R)
31 duplicate ;ABS(R>, ABS(R)
EA recal1_MA ;ABS(R). ABS(R). E»R
2A abs .ABS(R). ABS(R), ABS(E»R>
03 subtract ; ABS(R). ABS(R)-ABS(E»R>
37 Bt.zero ;ABS(R>. ABS(R)>ABS(E»R)?
0004 jump.true,ELL_i ;ABS(R) (Переход, если
;ABS(R)>ABS(E*R)
02 delete ;Стек пуст.
EA recall.MA ;E»R
2A abs ; ABS(E*R)
ELL_i ;Ha стеке содержится некое число
;W, которое равно либо ABS(R).
;либо ABS(E»R) в зависимости от
: того, какое из них больше.
28 sqr ; SQR(W)
A3 C0nst_Pl/2 ; SQR(W>. PI/2
04 multiply ;SQR(W)»PI/2
38 endcaic ;SQR(W)»PI/2
34 INC (HL) ;'при выходе из калькулятора
;регистровая пара HL всегда
.указывает на первый байт (байт
; экспоненты) числа, находящегося
;на вершине стека калькулятора.
;Увеличение экспоненты на едини-
; ыу, эквивалентно умножению чис-
,ла на 2. Итак, теперь на стеке:
; SQR (W) »Р1.
; Мы получили ту эмпирическую
■Формулу (см. выше), с помощью
; которой можно определить сколь-
, ко отрезков прямых нужно для
; изображения окружности или
; эллипса.
CDD52D CALL FP_TO_a; Выражение SQR(W)»PI округля-
;ется до ближаишего целого и пе-
;редается в аккумулятор проиес-
; сора.
3806 JR С.ELL.FC ;Если включился Флаг переноса,
:значит число оказалось больше
;255. а нам столько отрезков не
; нужно.
E6FC AND FC ; Два младших бита принудительно
;гасятся для того, чтобы
;результат был кратен четырем.
С604 ADD А.04 .Округляем результат вверх до
;ближайшего целого, делящегося
: на четыре.
3002 JR NC. ELL.DRAW ; Если <256. то переход.
3EFC ELL-FC LD A.FCH ;Если число отрезков >255. то
;выставляем 252. считая, что нан
; этого достаточно.
F5 ELL.DRAW PUSH AF ; Запомнили число отрезков на
;машинном стеке.
CD282D CALL STACK^А; И поместили его на стек кальку-
; лятора.
EF RST 28 ; Включение калькулятора. На сте-
; ке число Н - количество отрез-
;ков. с помошью которых аппрок-
; синируется эллипс или окруж-
; ность.
A3 const.Pi/2 ;N. PI/2
38 endcalc ;N. PI/2 - выход из калькулято-
ра. Пара HL указывает на байт
; экспоненты числа на вершине
; стека.
3683 LD (HL). 83Н ;После этого на вершине стека:
; N. 2«FI
EF RST 26 ;N. 2«FI
01 exchanee ;2»FI. N
05 divide ;2*PI/N - получили величину шага
; no углу для построения Н-уголь-
; ника
cf store.mf ;Запоннили шаг по углу в ячейке
; памяти калькулятора MF.
02 delete ;Стек пуст.
36 endcaic ;
CD???? CALL NXT.POINT ;Процедура возвращает экранные
.координаты XI и Y1 последней
;точки эллипса в ячейках памяти
; калькулятора НЮ и НИ.
Cl POP ВС ; Сняли с машинного стека ранее
;сохраненное там число N и взяли
;его в регистр В для организации
;цикла построения N-угольника.
С5 ELL.LOOF PUSH ВС ;
EF RST 26 ;
ЕЕ recal1_МЕ ;А1 - текущий угол.
EF recal1.HF ;Ai. INCR - шаг по углу.
OF add i Al + INCR
СЕ store.HE ;B ячейку НЕ заносится новое из-
мененное значение текущего уг-
; ла.
02 delete ;Стек пуст.
FO recall .ню ,Х1
Fl recail_Mil .X1.Y1
CD???? CALL NXT.POINT ;Теперь эта процедура возвращает
;экранные координаты Х2 и Y2
:в ячейках МЮ и Mil.
EF RST 28 ;XI. Yl
FO recal1.M10 ;XI. Yl. X2
Fi recall_Hll ;XI. Yl, X2. Y2
CD???? CALL CLIP ;Вызов процедуры изображения
; отрезка.
Cl FOF ВС ; В - счетчик сторон N-угольника.
юеу djnz ell_loop .Возврат на повтор, если не все
;стороны нарисованы.
С9 RET ;Возврат в БЕЙСИК.
Процедура NXT.POINT
Код Метка мнемоника комментарий (стек калькулятора»
EF EL_MAIN RST 28 ,Включение калькулятора.
ЕА recal1-МА ;E«R
ЕЕ recal1_МЕ ;E«R, А1
20 cos ;E«R. COS(Al)
04 multiply ;E«R«COS(Al>
C8 store_M8 :ячейка памяти И8 временно ис-
,пользуется не по основному наз-
;начению для хранения числа
; E«R«COS(Al>.
ЕС recall-НС !E«R«COS(А1).COS(А)
04 multiply i E«R«C0S(A1)"COS(А)
ЕВ recall_МВ ; E«R«COS(A1)"COS(A). R
EE recall-ME ;E«R«COS(Al>»COS(A>.R.Al
IF Sin ;E»R«C0S(A1)«C0S(A>.R. SIN(Al)
04 multiply ;E«R»COS(Al)«COS(A).R*SIN<Al)
C9 store_M9 ;B M9 запоминается R«SIN(A1>
ED recall-MD ; E«R«COS(A1)*COS(A). R*SIN(A1).
. SIN(A)
04 multiply ;E»R»COS(A1)«COS(A),R'SIN(A1)«
i«SXK(A)
03 subtract ;E«R«COS(Al)»COS(A) - R«SIN(A1)«
;«SIN(A)
F2 recal1_M12 : E«R»C0S(A1)"COS(A) - R«SIN(A1)«
;«SIN(A).X
OF add ;X ♦ E«R«C0S(A1)«COS(A) -
;-R»SIN(A1)«SIN(A)
DO store-m10 ;Полученное значение равно гори-
i зонтальной экранной координате
; вершины многоугольника, она
; сохраняется в НЮ.
02 delete ;Стек пуст.
Ев recall.не ;E«R«COS(Al)
ED recal1JTO ;E»r«COS(al).SIN(a)
04 multiply ;E«R*C0S(A1)«SIH(A)
E9 recal1_H9 ; E»R»COS(A1)«SIN(A). R«SIH(A1)
EC recall_HC ;E«R«COS<Al)«SIH(A).R«SIH(Al).
;C0S<A)
04 multiply ; E»R»COS(A1)«SIN(a). R»SIN(A1)»
; «COS(A)
OF add ; E<R<C0S<A1)«SIN(A)*R«SIN(A1)*
; «COS (A)
F3 recal1_H13 ;E«R»COS(Al)»SIH(A)*R»SIN(Al>»
; «COS(A)> Y
OF add ;Y»E«R«C0S(A1)«SIN(A)+R*SIN(A1)«
;«COS(A)
Di store.Hil ;полученное значение равно вер-
.тикальнои экранной координате
;вершины многоугольника, она
сохраняется в НИ.
02 delete ;Стек пуст.
3S endcalc
С9 RET ; Возврат в вызывающую процедуру.
Специально для тех наших читателей, кто еше не освоил про-
граммирование в машинных кодах и кодах встроенного калькулятора
мы привели реализацию того же самого алгоритма на БЕИСИКе.
1 def fn x(s.k, j.m.n) = j+(127. 5«s-K)«(n-j)/(m-K): reh эта
функция аналогична процедуре convex.
2 DEF FN Y(t.K. J.m.n) = KM87. 5«t-J)«(m-K)/(n-J): REH эта
функция аналогична процедуре COHV_Y.
3 DEF FN a(x.е.г.э.Ь) - x*e»r«C0S(b)»C0S(a)-r«siH(b)*siH(a):
REH эта Функция применяется при построении окружностей и
эллипсов и является аналогом первой половины процедуры
NXT_P0IHT.
4 DEF FN Ь(у. е. г, а. Ы = y*e«r«COS(b)«SXN(a)+r«SIH(b)»COS(a)
КЕН функция является аналогом второй половины процедуры
HXTPOIHT.
10 CLS
20 PFIHT AT 7.8: "Press n for ИНе"
30 PRIST AT 9.6: 'Press с for Circle"
40 PRIHT AT 11.6: "Press e for Ellipse"
50 LET a* S IHKEY*
60 IF a» = "n" THEN GO TO 100
70 IF a* = "C" OR a» ="e" THEN GO TO 200
80 GO TO 50
97 REM
98 REH*»»■»»»■»«»»»»»»»■«»■■»■■»»»»■»■».............
99 REM
100 CLS
110 IHPUT "Xl=?":xl
120 IHPUT "Yl = ?"; У1
130 IHPUT тхг-?": X2
140 IHPUT "Y2=?";y2
150 GO SUB 1000
160 STOP
197 REM
198 .............................................
199 REM
200 CLS
210 IHPUT "R=?":r
220 IHPUT "X=?":x
230 IHPUT "?=?";у
240 IF a» ="C" THEN LET e=i: LET a=0: GO TO 270
250 IHPUT "E^?";e
260 IHPUT "A-?":a
270 GO SUB 2000
280 STOP
997 REH
998 REH Подпрограмма аналогична процедуре CLIP
999 REH
1000 LET xi * xl-127. 5: LET yl = у1-87. 5:
LET x2 г x2-127. 5: LET у2 = у2-67. 5
1010 GO SUB 1500
1020 IF (Sl»s£-l)»(tl»tE-l)=0 THEH RETURH
1030 IF 31 = 0 THEH GO TO 1060
1040 LET yl=FH XiSl.Xl. y1.x2,y2): LET Xl = 127. 5»sl
1050 GO SUB 1500
1060 IF tl-0 THEN GO TO 1080
1070 LET Xl = FH y(tl.Xl. y1.x2. y2): LET yl = 87. 5»tl
1080 IF 32=0 THEH GO TO 1110
1090 LET YE=FH X(S2. xl. У1.Х2,У2): LET X2=1E7. 5«sE
1100 GO SUB 1500
1110 IF t£=0 THEH GO TO 1130
1120 LET XE=FN Y(t2, xl. Yl. x2. У21: LET y2 = 87. 5*t2
ИЗО GO SUB 1500
1140 IF S1<>0 OR tl<>0 OR s2<>0 OR t2<>0 THEH RETURH
1150 LET XE-IHT(X2*128): LET X1=IHT(X1*128):
LET Y2=IHT(Y2*88): LET У1 = 1НТт*в8)
1160 PLOT Xl.Yl
1170 DRAW X2-X1.Y2-Y1
1180 RETURH
1497 REH
1498 REH Подпрограмма аналогична процедуре PARAHS
1499 REH
1500 LET 31 = 0: LET 32=0: LET tl = 0: LET t2=0
1510 IF XI <-127. 5 THEH LET Si = -1
1520 IF XI > 127. 5 THEH LET 31 = 1
1530 IF X2 <-127.5 THEH LET 32 = -1 "
1540 IF X2 > 127. 5 THEH LET S2 = 1
1550 IF Yl <-87.5 THEH LET tl =-1
1560 IF Yl > 87.5 THEH LET tl = 1
1570 IF y2 <-87. 5 THEH LET t2 = -1
1580 IF У2 > 127. 5 THEH LET t2 = 1
1590 RETURH
1997 REH
1998 REH Подпрограмма аналогична процедуре KL_HAIH
1999 REH
2000 LET n = PI»SQR(ABS(e«r))
2010 LET n = 4*(4«(IHT(n/4))>
2020 IF n>252 THEH LET n=252
2030 LET da=2*PI/n
2035 LET al=0
2040 FOR Z-1 TO П
2050 LET x l - FH a(x. e, r. a, al) '
2060 LET Ti = FH btr. e.r.a.ai)
2070 LET ai-ai+da
2060 LET x2 = FH a(x. е. r. a. al)
2090 LET У2 = FH Ъ(У. e. r. a. al)
2100 GO SUB 1000
2110 NEXT z
2120 RETURH
3.2. Масштабирование
Итак, мы с Вани научились изображать на экране любые от-
резки прямых, а не только те. которые полностью на этом экране
помешаются. Научившись изображать отрезки, можете считать, что
вы научились изображать любые геометрические фигуры или тела,
поскольку немного поработав с бумагой в клеточку вы сможете
представить любое тело в виде набора отрезков (правда это может
выглядеть грубовато, но это уже дело вкуса, терпения, таланта и
зависит от того, сколько оперативной памяти Вы готовы пожертво-
вать на хранение координат кондов своих отрезков и какое вам
нужно быстродействие).
Теперь оказывается, что то. как изображается отрезок на
экране, зависит не только от того, какие он имеет номинальные
размеры в массиве данных, а еше и от его положения относительно
наблюдателя и экрана. Существуют ведь законы проективной связи.
Естественно, чен дальше от Вас находится объект, тем меньше он
должен выглядеть на экране. Если вы. играя в игру типа "Звезд-
ных войн", подлетите на своен корабле к кораблю противника, то
он должен увеличиться в размерах, может быть на нем смогут поя-
виться новые конструкционные детали, может быть даже он станет
таким большим, что не впишется в Ваш экран и тогда процедуры
клиширования изображения "отрежут" ту часть, которая на экран
не попадает, так или иначе, но перед нами встает проблема мас-
штабирования изображения объекта на экране в зависимости от его
удаленности от экрана и от точки начала координат, в которой
находится наблюдатель.
Эта концепция будет Вам более понятна, если вы взглянете
на Рис. 27.
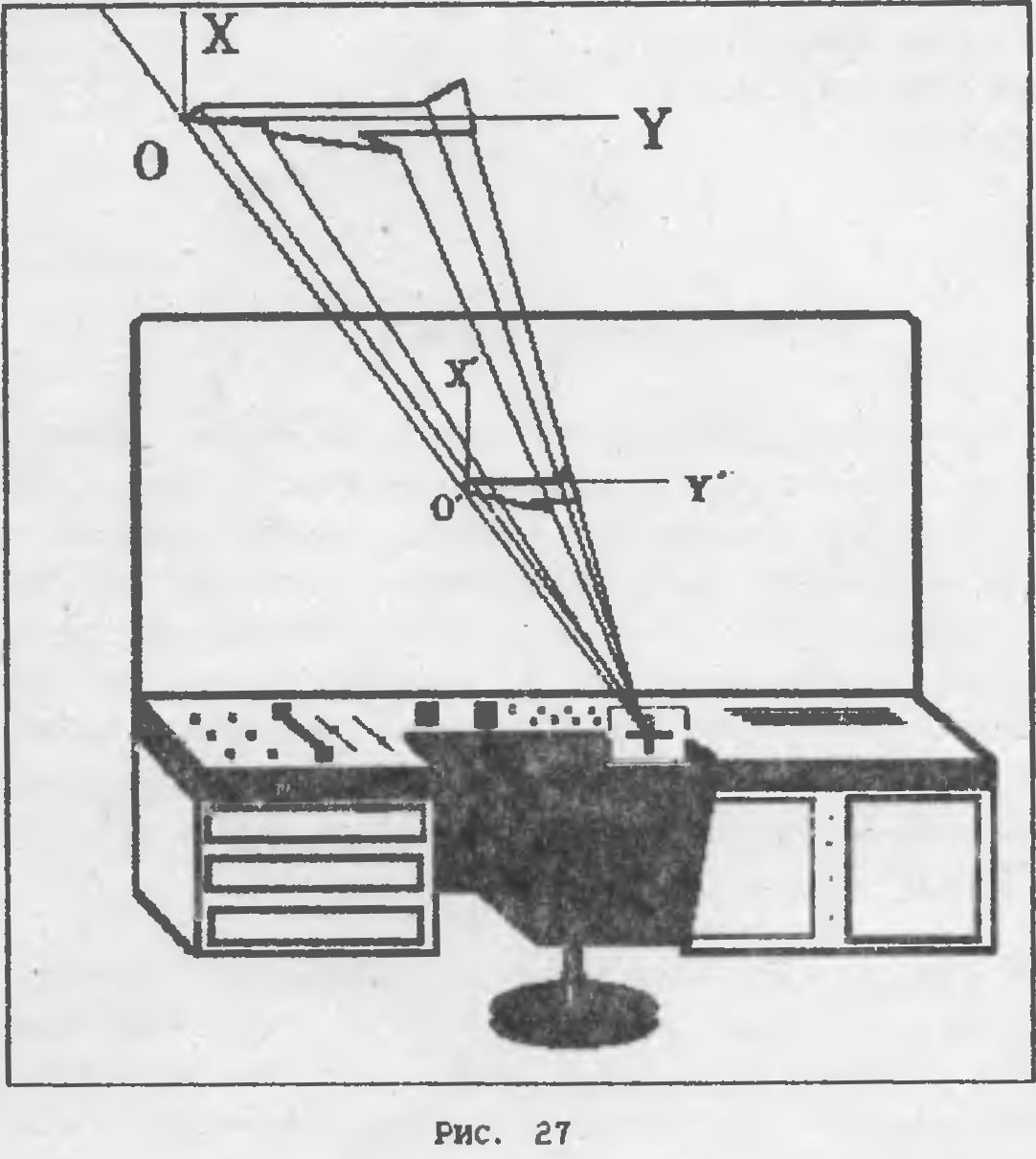
К счастью, определить экранные координаты трехмерного
объекта, удаленного в пространстве от Вас и от проекционного
экрана, оказывается очень просто, если предположить, что точка
начала координат и положение наблюдателя совпадают (а так оно в
большинстве случаев и есть). Формулы для расчета экранных коор-
динат оказываются довольно простыни, известными из элементарной
геометрии:
х'=xid/z;
Y'=Y<d/Z) m
Как видите, масштабирование изображения происходит в соот-
ветствии со значением d. которое вы выбрали сами. см. Рис. <?8.
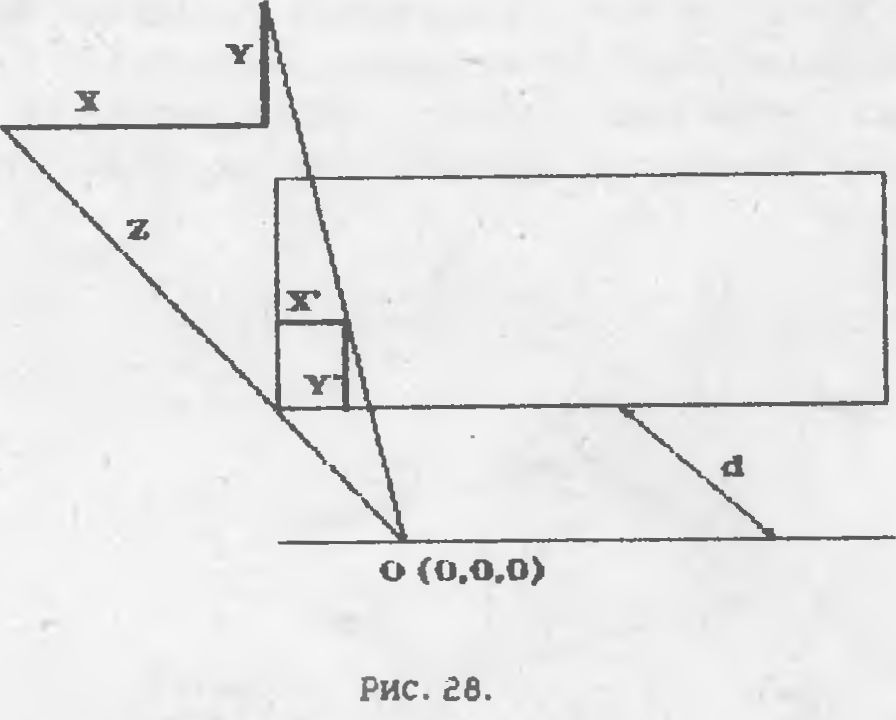
Чтобы трансформировать на экран не точечный объект, а
объемное тело, достаточно определить экранные координаты всех
его вершин и соединить их на экране отрезками прямых.